Tìm số hạng cuối của một cấp số cộng có 5 số hạng biết tổng số hạng đầu và số hạng thứ 3 là 28 và tổng số hạng thứ 3 và số hạng cuối là 40.
Theo đề bài ta có :
\(u_1+u_3=28\)
\(\Leftrightarrow u_1+u_1+2d=28\)
\(\Leftrightarrow2u_1+2d=28\left(1\right)\)
\(u_3+u_5=40\)
\(\Leftrightarrow u_1+2d+u_1+4d=40\)
\(\Leftrightarrow2u_1+6d=40\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}2u_1+2d=28\\2u_1+6d=40\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}d=3\\u_1=11\end{matrix}\right.\)
Số hạng cuối \(u_5=u_1+4d=11+4.3=23\)
Đúng 2
Bình luận (0)
\(x>2\Rightarrow\lim\limits_{x\rightarrow2^+}\dfrac{x\left(x-2\right)}{x-2}=x=2\)
\(x< 2\Rightarrow\lim\limits_{x\rightarrow2^-}\dfrac{x\left(x-2\right)}{-\left(x-2\right)}=-x=-2\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}\dfrac{x^2-2x}{\left|x-2\right|}=2\ne\)\(\lim\limits_{x\rightarrow2^-}\dfrac{x^2-2x}{\left|x-2\right|}=-2\)
\(\Rightarrow\lim\limits_{x\rightarrow2}\dfrac{x^2-2x}{\left|x-2\right|}\) không tồn tại
Đúng 1
Bình luận (0)
\(\lim\limits_{x\rightarrow3^+}\dfrac{x^2-9}{x-3}=\)\(\lim\limits_{x\rightarrow3^+}\dfrac{\left(x-3\right)\left(x+3\right)}{x-3}=\)\(\lim\limits_{x\rightarrow3^+}x+3=6\)
\(\lim\limits_{x\rightarrow3^-}4x-5=7\)
\(\Rightarrow\lim\limits_{x\rightarrow3^+}f\left(x\right)\ne\)\(\lim\limits_{x\rightarrow3^-}f\left(x\right)\)
\(\Rightarrow f\left(x\right)\) không liên tục tại \(x=3\)
\(\Rightarrow\) Không tồn tại \(\lim\limits_{x\rightarrow3}f\left(x\right)\)
Đúng 1
Bình luận (0)
 mn giúp em bài 2 2 ý đc ko ạ
mn giúp em bài 2 2 ý đc ko ạ
Bài 2:
1: \(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+3\end{matrix}\right.\)
=>\(u_2=u_1+3=4;u_3=u_2+3=4+3=7\)
\(u_4=u_3+3=7+3=10;u_5=u_4+3=10+3=13\)
=>\(u_n=1+3\left(n-1\right)=1+3n-3=3n-2\)
2: \(\left\{{}\begin{matrix}u_1=3\\u_{n+1}=4u_n\end{matrix}\right.\)
=>\(u_2=4\cdot u_1=4\cdot3=12;u_3=4\cdot u_2=4\cdot12=48\); \(u_4=4\cdot u_3=4\cdot48=192;u_5=4\cdot u_4=4\cdot192=768\)
=>Công thức là \(u_n=3\cdot4^{n-1}\)
Đúng 1
Bình luận (0)
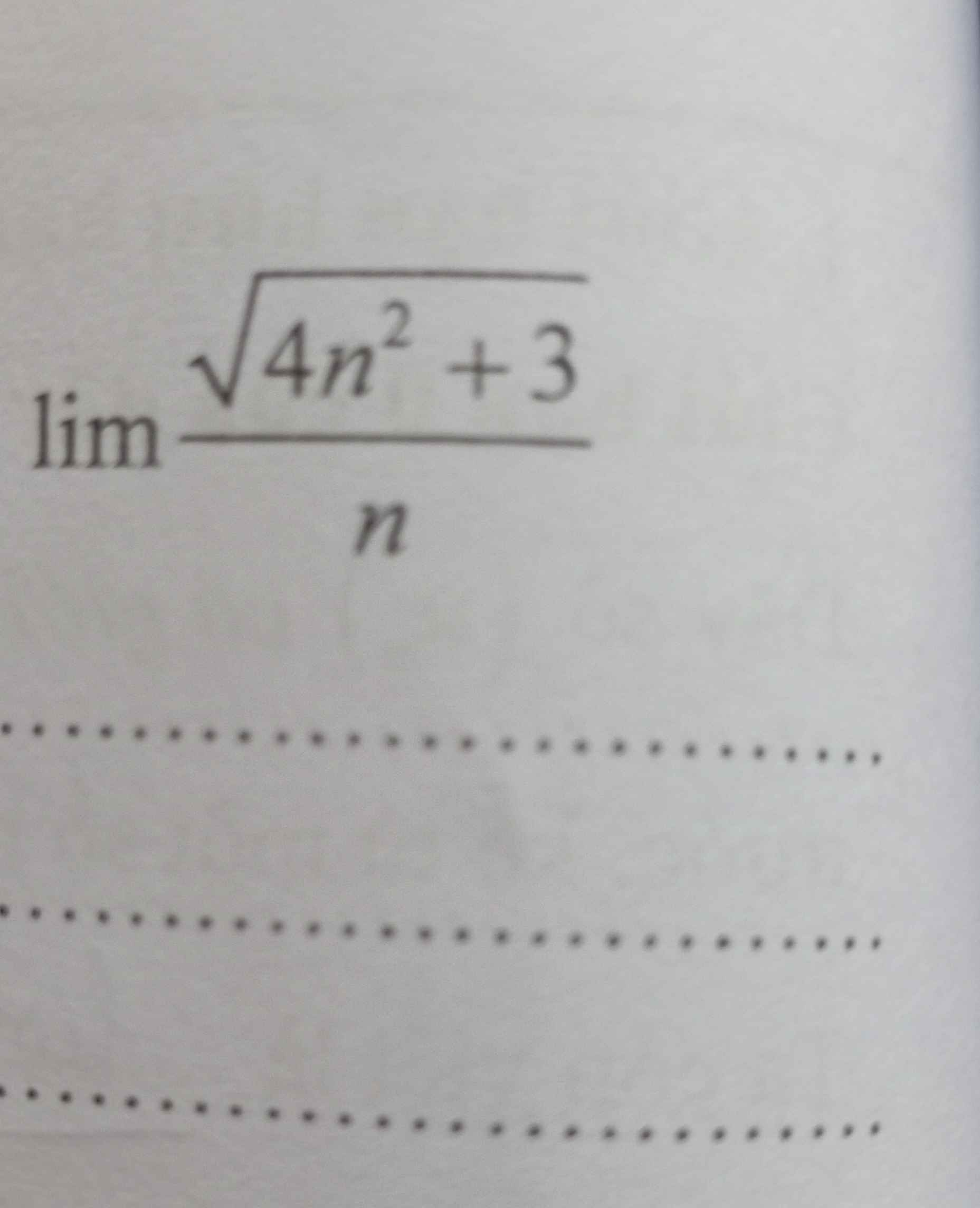 Tính giới hạn sau:
Tính giới hạn sau:
\(...=\lim\limits_{n\rightarrow\infty}\dfrac{\sqrt{n^2\left(4+\dfrac{3}{n^2}\right)}}{n}=\)\(\lim\limits_{n\rightarrow\infty}\dfrac{\left|n\right|\sqrt{4+\dfrac{3}{n^2}}}{n}\)
\(=\left[{}\begin{matrix}\lim\limits_{n\rightarrow+\infty}\dfrac{n\sqrt{4+\dfrac{3}{n^2}}}{n}=\dfrac{2}{1}=2\\\lim\limits_{n\rightarrow-\infty}\dfrac{-n\sqrt{4+\dfrac{3}{n^2}}}{n}=-\dfrac{2}{1}=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
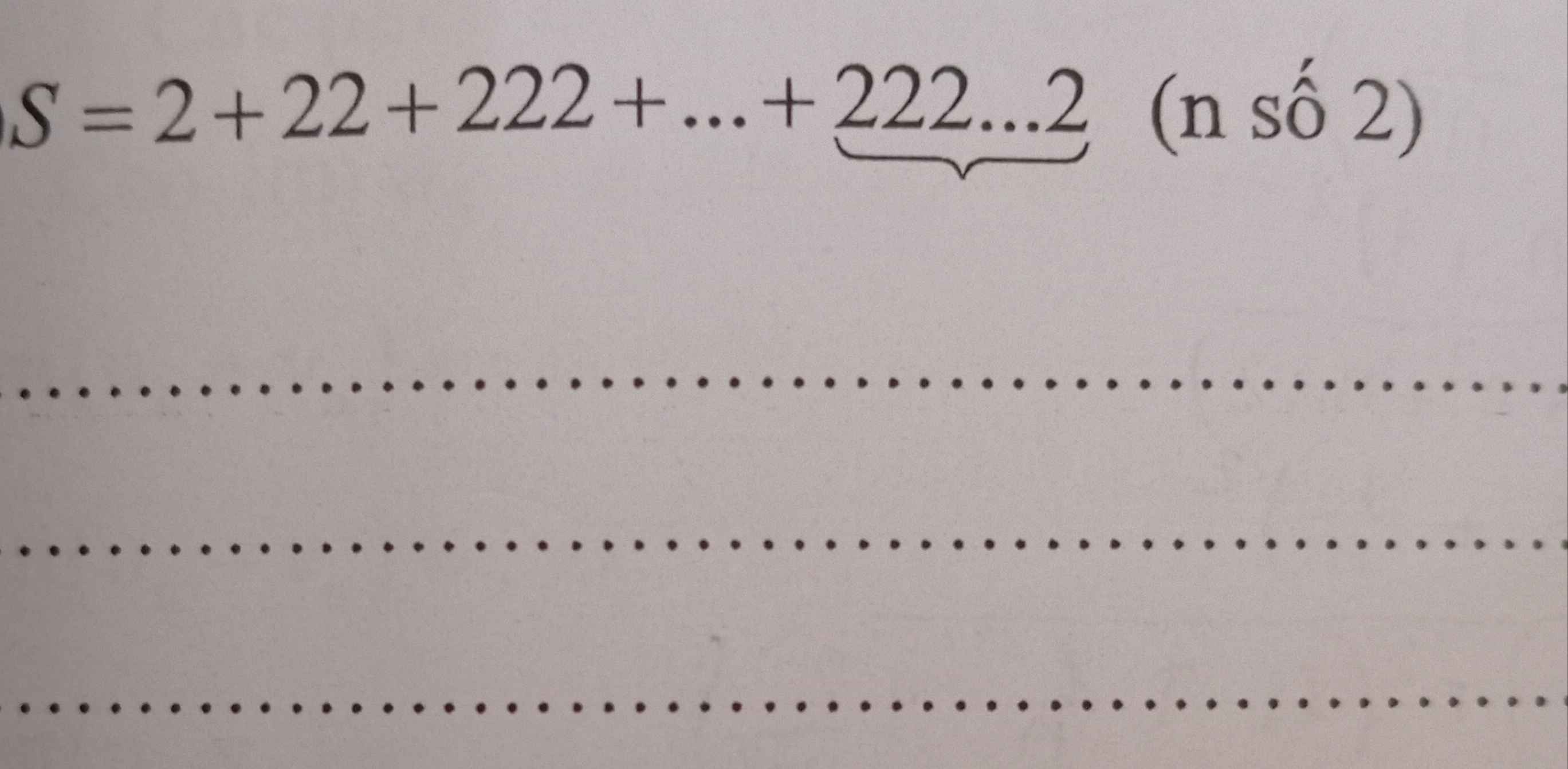 Tính các tổng sau:
Tính các tổng sau:
\(S=2\left(1+11+111+...+111...1\right)\left(n.số.1\right)=2A\)
\(A=1+11+111+...+111...1\left(n.số.1\right)\)
\(\Rightarrow9A=9+99+999+...+999...9\left(n.số.9\right)\)
\(\Rightarrow9A=\left(10-1\right)+\left(100-1\right)+\left(1000-1\right)+...+\left(10^n-1\right)\)
\(\Rightarrow9A=\left(10+100+1000+...+10^n\right)-n\)
\(B=10+100+1000+...+10^n\)
\(u_1=10;q=10\)
Áp dụng công thức tính tổng \(n\) số hạng đầu của cấp số nhân:
\(B=\dfrac{10\left(1-10^n\right)}{1-10}=\dfrac{10\left(10^n-1\right)}{9}\)
\(\Rightarrow9A=B-n=\dfrac{10\left(10^n-1\right)}{9}-n=\dfrac{10\left(10^n-1\right)-9n}{9}\)
\(\Rightarrow A=\dfrac{10\left(10^n-1\right)-9n}{81}\)
\(\Rightarrow S=2A=\dfrac{2.\left[10\left(10^n-1\right)-9n\right]}{81}=\dfrac{20\left(10^n-1\right)-18n}{81}\)
Đúng 2
Bình luận (0)
Cho cấp số cộng (Un) biết U1 =2; d=3
a) Cho Sn = 260. Tìm n
b) Tính S= U60 + U61 + U62 +... +U80
a: \(S_n=260\)
=>\(n\cdot\dfrac{\left[2u_1+\left(n-1\right)d\right]}{2}=260\)
=>\(n\cdot\dfrac{2\cdot2+\left(n-1\right)\cdot3}{2}=260\)
=>\(n\left(4+3n-3\right)=520\)
=>\(3n^2+n-520=0\)
=>\(3n^2-39n+40n-520=0\)
=>(n-13)(3n+40)=0
=>\(\left[{}\begin{matrix}n=13\left(nhận\right)\\n=-\dfrac{40}{3}\left(loại\right)\end{matrix}\right.\)
b:
Số số hạng trong dãy là 80-60+1=20+1=21(số)
\(S=u_{60}+u_{61}+...+u_{80}\)
\(=u_1+59d+u_1+60d+...+u_1+79d\)
\(=21u_1+d\left(59+60+...+79\right)\)
\(=21\cdot2+3\cdot\dfrac{\left(79+59\right)\cdot21}{2}\)
=42+4347
=4389
Đúng 2
Bình luận (0)
Tính các tổng sau:
a) S = 1+2+4+8+...+2^63
b) S = 1+10+100+...+1000000
a: \(S=1+2+4+...+2^{63}\)
=>\(S=1+2+2^2+...+2^{63}\)
=>\(2S=2+2^2+2^3+...+2^{64}\)
=>\(2S-S=2+2^2+...+2^{64}-1-2-...-2^{63}\)
=>\(S=2^{64}-1\)
b: \(S=1+10+100+...+1000000\)
=>\(S=10^0+10^1+...+10^6\)
=>\(10S=10+10^2+...+10^7\)
=>\(10S-S=10+10^2+...+10^7-10^0-10^1-...-10^6\)
=>\(9S=10^7-1\)
=>\(S=\dfrac{10^7-1}{9}\)
Đúng 2
Bình luận (0)
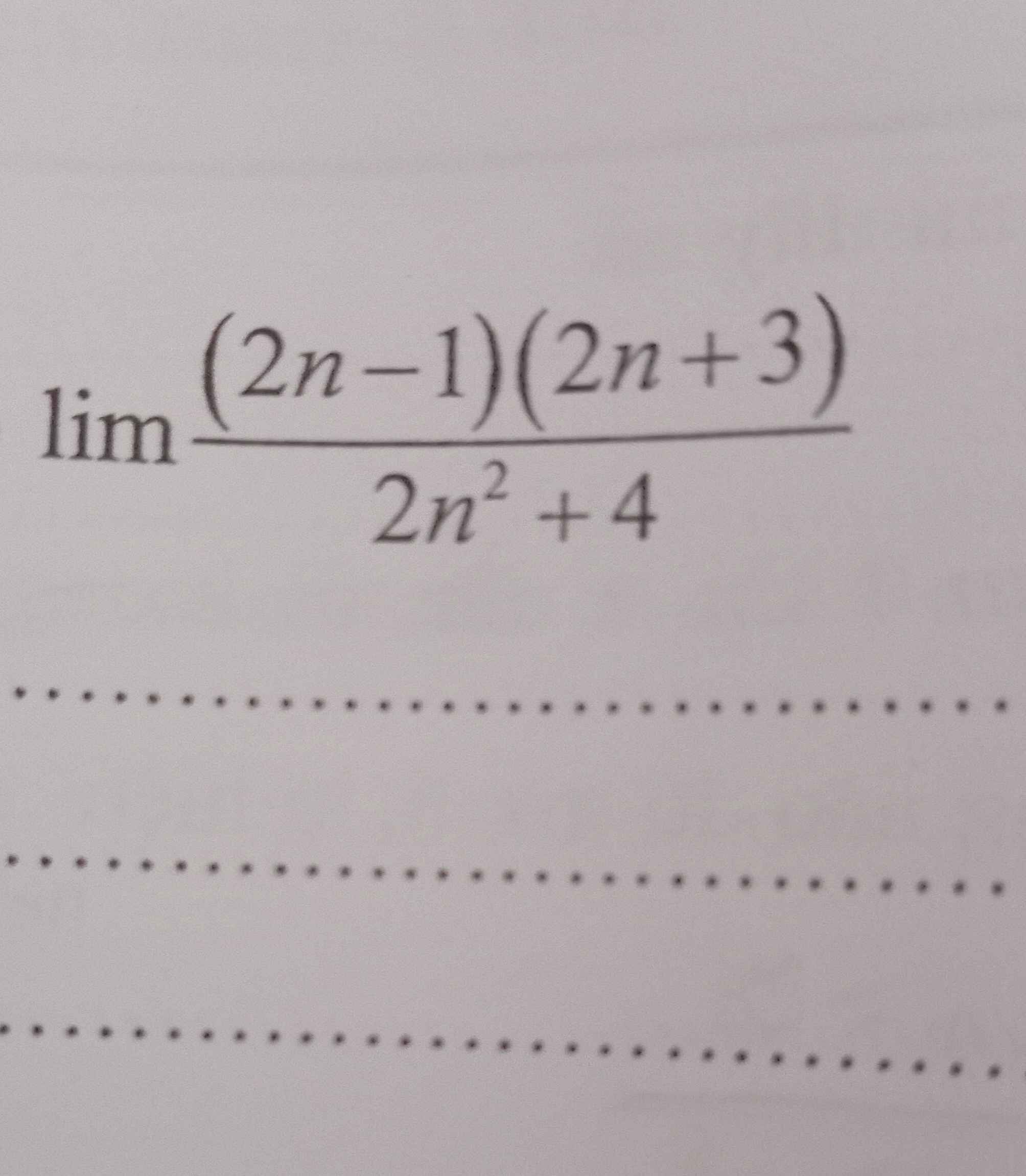 Tính giới hạn sau:
Tính giới hạn sau:
\(\lim\limits\dfrac{\left(2n-1\right)\left(2n+3\right)}{2n^2+4}\)
\(=\lim\limits\dfrac{4n^2+6n-2n-3}{2n^2+4}\)
\(=\lim\limits\dfrac{4n^2+4n-3}{2n^2+4}\)
\(=\lim\limits\dfrac{4+\dfrac{4}{n}-\dfrac{3}{n^2}}{2+\dfrac{4}{n^2}}=\dfrac{4}{2}=2\)
Đúng 2
Bình luận (0)
\(...=\lim\limits_{n\rightarrow\infty}\dfrac{4n^2+4n-3}{2n^2+4}=\)\(\lim\limits_{n\rightarrow\infty}\dfrac{n^2\left(4+\dfrac{4}{n}-\dfrac{3}{n^2}\right)}{n^2\left(2+\dfrac{4}{n^2}\right)}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{4+\dfrac{4}{n}-\dfrac{3}{n^2}}{2+\dfrac{4}{n^2}}=\dfrac{4}{2}=2\)
Đúng 1
Bình luận (0)
Cho a, b, c lập thành một cấp số nhân. Chứng minh: (a + b2)(b2+ c2) = (ab +bc)2
Đề sai em, đề đúng phải là \(\left(a^2+b^2\right)\left(b^2+c^2\right)=\left(ab+bc\right)^2\)
Em thiếu dấu bình phương của a
Đúng 0
Bình luận (1)











