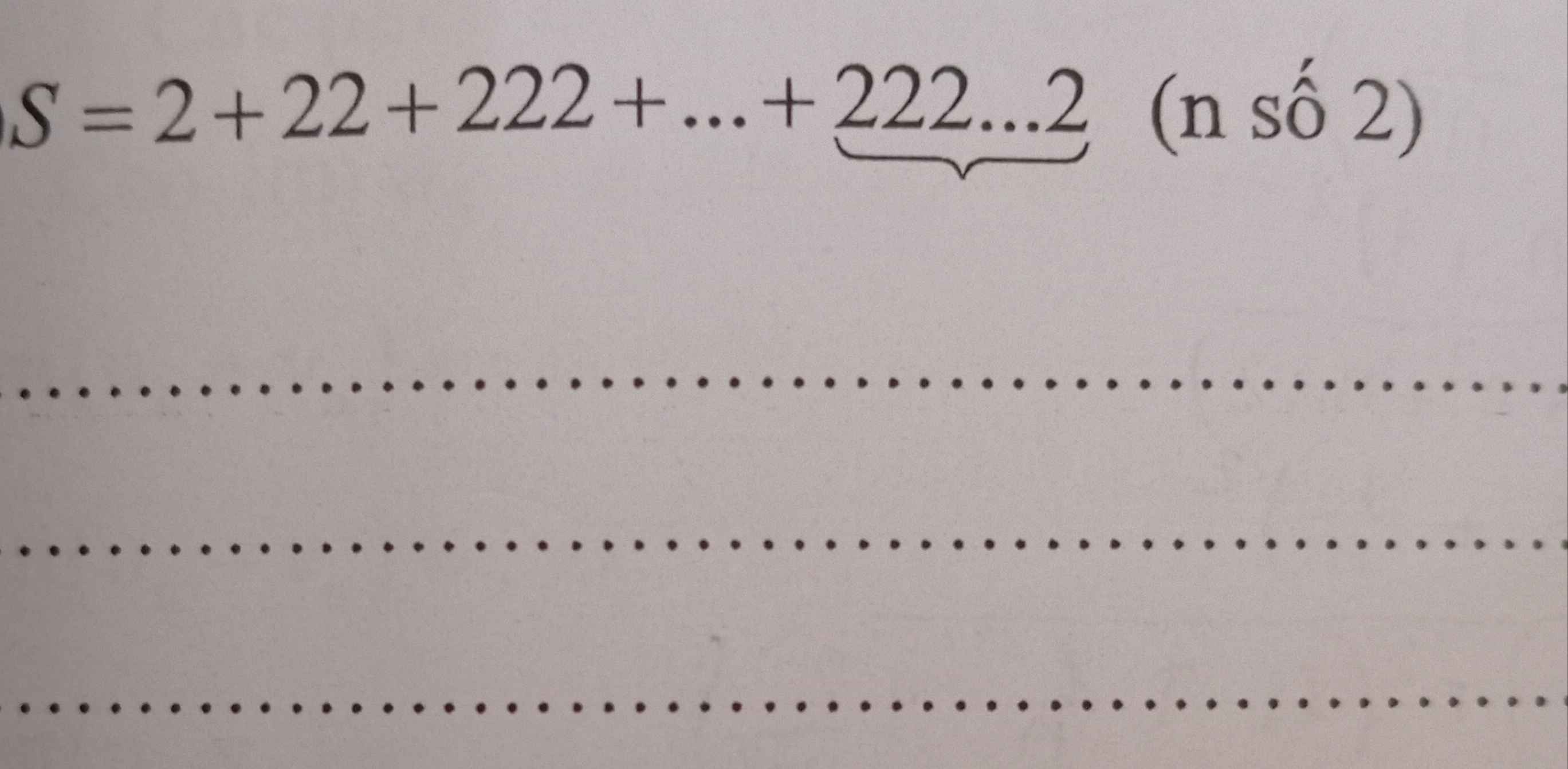\(S=2\left(1+11+111+...+111...1\right)\left(n.số.1\right)=2A\)
\(A=1+11+111+...+111...1\left(n.số.1\right)\)
\(\Rightarrow9A=9+99+999+...+999...9\left(n.số.9\right)\)
\(\Rightarrow9A=\left(10-1\right)+\left(100-1\right)+\left(1000-1\right)+...+\left(10^n-1\right)\)
\(\Rightarrow9A=\left(10+100+1000+...+10^n\right)-n\)
\(B=10+100+1000+...+10^n\)
\(u_1=10;q=10\)
Áp dụng công thức tính tổng \(n\) số hạng đầu của cấp số nhân:
\(B=\dfrac{10\left(1-10^n\right)}{1-10}=\dfrac{10\left(10^n-1\right)}{9}\)
\(\Rightarrow9A=B-n=\dfrac{10\left(10^n-1\right)}{9}-n=\dfrac{10\left(10^n-1\right)-9n}{9}\)
\(\Rightarrow A=\dfrac{10\left(10^n-1\right)-9n}{81}\)
\(\Rightarrow S=2A=\dfrac{2.\left[10\left(10^n-1\right)-9n\right]}{81}=\dfrac{20\left(10^n-1\right)-18n}{81}\)