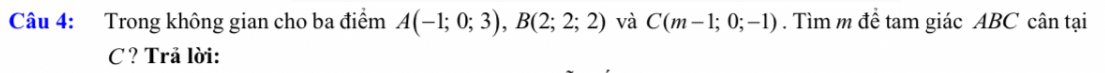
\(AC=\sqrt{\left(m-1+1\right)^2+\left(0-0\right)^2+\left(-1-3\right)^2}=\sqrt{m^2+16}\)

\(BC=\sqrt{\left(m-1-2\right)^2+\left(0-2\right)^2+\left(-1-2\right)^2}=\sqrt{\left(m-3\right)^2+13}=\sqrt{m^2-6m+22}\)

Để \(\Delta ABC\) cân tại \(C\) khi và chỉ khi

\(\Leftrightarrow AC=BC\)

\(\Leftrightarrow\sqrt{m^2+16}=\sqrt{m^2-6m+22}\)

\(\Leftrightarrow m^2+16=m^2-6m+22\left(m^2+16>0\right)\)

\(\Leftrightarrow6m=6\)

\(\Leftrightarrow m=1\)

Vậy \(m=1\) thỏa mãn đề bài

\(\overrightarrow{MQ}=\left(400;200;2\right)\)

Vectơ vận tốc chuyển động có tọa độ:

\(\overrightarrow{v}=\dfrac{\overrightarrow{MQ}}{10}=\dfrac{\left(400;200;2\right)}{10}=\left(40;20;0,2\right)\) \(\left(km/phút\right)\)

Ta có thời gian từ \(M\rightarrow N\) là \(30\left(phút\right)\)

\(\Rightarrow\overrightarrow{MN}=30.\overrightarrow{v}=30.\left(40;20;0,2\right)=\left(1200;600;6\right)\)

\(\Leftrightarrow\left(a-1000;b-600;c-14\right)=\left(1200;600;6\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}a-1000=1200\\b-600=600\\c-14=6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=2200\\b=1200\\c=20\end{matrix}\right.\) \(\Leftrightarrow N\left(2200;1200;20\right)\)

\(\Rightarrow S=a+b+2c=2200+1200+2.20=3440\)

a) \(f\left(100\right)=0,001.100^2+0,5.100+18=78\left(triệu.đồng\right)\Rightarrow\) Đúng

b) Lợi nhuận \(h\left(x\right)=g\left(x\right)-f\left(x\right)=4x+50-\left(0,001x^2+0,5x+18\right)=-0,001x^2+3,5x+32\)

HS \(h\left(x\right)\) là 1 Parabol có phần lõm hướng xuống, hoành độ điểm cực đại là

\(x=-\dfrac{b}{2a}=-\dfrac{3,5}{2.\left(-0,001\right)}=1750\left(sản.phẩm\right)\)

\(\Rightarrow\) Đúng

c) \(h\left(x\right)_{max}=h\left(1750\right)=-0,001.1750^2+3,5.1750+32=3094,5\left(triệu.đồng\right)\)

\(\Rightarrow\) Đúng

d) \(h\left(500\right)=1532\)

\(h\left(600\right)=1772\)

\(\Rightarrow h\left(600\right)>h\left(500\right)\)

\(\Rightarrow\) Đúng

\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(2^{\dfrac{3x-2}{x-1}}+1\right)=+\infty\left(1\right)\)

\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^2-3x-1}{x-1}=\lim\limits_{x\rightarrow1^-}x+1-\dfrac{2}{x-1}=-\infty\left(2\right)\)

\(\Rightarrow x=1\) là tiệm cận đứng của \(f\left(x\right)\) và \(TCX:y=x+1\left(x< 1\right)\)

Khi \(x>1:\)

\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\left(2^{\dfrac{3x-2}{x-1}}+1\right)=2^3+1=9\)

Khi \(x< 1:\) Không có \(TCN\) (vì là hàm bậc 2 trên bậc 1)

\(\Rightarrow TCN:y=9\left(x>1\right)\)

\(\left(1\right);\left(2\right)\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne f\left(1\right)=12\)

\(\Rightarrow\) HS \(f\left(x\right)\) không liên tục tại \(x=1\)

Đồ thị \(3\) đường tiệm cận \(\left\{{}\begin{matrix}y=x+1\left(x< 1\right)\\y=9\left(x>1\right)\\x=1\end{matrix}\right.\)

Dựa vào đồ thị ta thấy \(3\) đường tiệm cận không cắt nhau tại \(3\) điểm để tạo thành tam giác

Vậy :

a) Sai

b) Sai

c) Sai

d) Đúng

a) Ta thấy đây là một tổng của cấp số nhân lùi vô hạn với:

\(\left\{{}\begin{matrix}u_1=1\\q=\dfrac{2}{3}\left(\left|q\right|< 1\right)\end{matrix}\right.\)

\(\Rightarrow S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\dfrac{2}{3}}=3\)

b) \(...\Rightarrow S=2\left[1-\dfrac{3}{4}+\left(\dfrac{3}{4}\right)^2-\left(\dfrac{3}{4}\right)^3+...\right]=2T\)

Ta thấy \(T\) cũng là một tổng của cấp số nhân lùi vô hạn với :

\(\left\{{}\begin{matrix}u_1=1\\q=-\dfrac{3}{4}\left(\left|q\right|< 1\right)\end{matrix}\right.\)

\(\Rightarrow T=\dfrac{u_1}{1-q}=\dfrac{1}{1-\left(-\dfrac{3}{4}\right)}=\dfrac{4}{7}\)

\(\Rightarrow S=2T=2.\dfrac{4}{7}=\dfrac{8}{7}\)

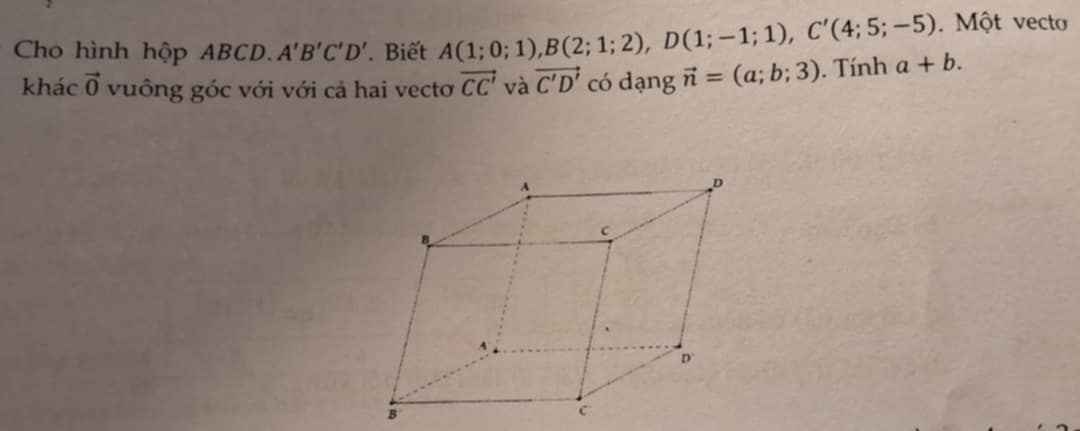
\(\overrightarrow{CC'}=\overrightarrow{AC'}-\overrightarrow{AC}=C'\left(4;5;-5\right)-A\left(1;0;1\right)=\left(3;5;-6\right)\)

\(\overrightarrow{C'D'}=-\overrightarrow{AB}=-\left(1;1;1\right)=\left(1;1;1\right)\)

\(\overrightarrow{n}\perp\overrightarrow{CC'}\Leftrightarrow3a+5b-18=0\left(1\right)\)

\(\overrightarrow{n}\perp\overrightarrow{C'D'}\Leftrightarrow a+b+3=0\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}3a+5b-18=0\\a+b+3=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{33}{2}\\b=\dfrac{27}{2}\end{matrix}\right.\)

\(\Rightarrow a+b=-\dfrac{33}{2}+\dfrac{27}{2}=-3\)