Người hay giúp bạn khác trả lời bài tập sẽ trở thành học sinh giỏi. Người hay hỏi bài thì không. Còn bạn thì sao?
Hình thang có nhiều nhất bao nhiêu góc nhọn, bao nhiêu góc tù? Vì sao?
Được cập nhật Hôm kia lúc 12:17 0 câu trả lời
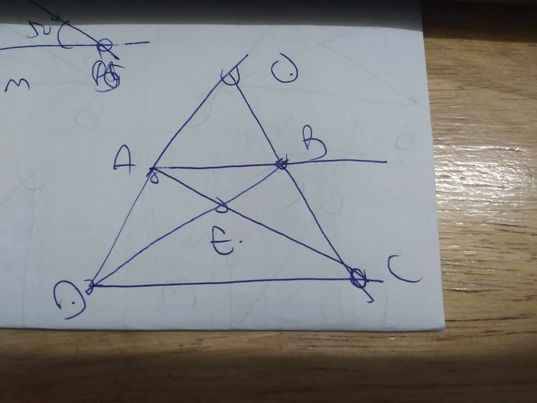
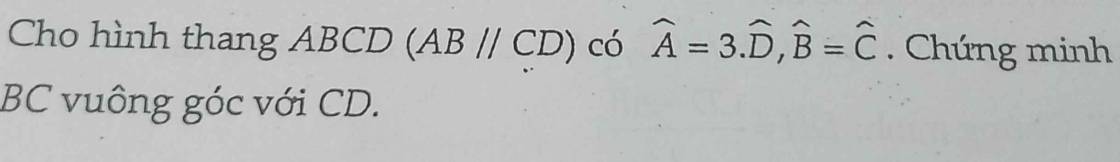cho hình thang ABCD (AB//CD) có các tia phân giác của các góc A và D gặp nhau tại điểm I thuộc cạnh bên BC . chúng minh rằng AD bằng tổng của 2 cạnh đáy
Được cập nhật Hôm kia lúc 12:15 0 câu trả lời
Cho hình thang vuông ABCD có góc A = góc D = 90 độ, AB = 5cm, AD = 12cm, BC=13cm. Tính CD= ?
Được cập nhật Hôm kia lúc 11:59 2 câu trả lời
Xét \(\Delta ABD\) :
Áp dụng định lý py - ta - go ta có :
\(BD^2=AB^2+AD^2\)
\(BD^2=5^2+12^2=169\)
\(BD=13cm\)
\(\Rightarrow BD=BC\)
\(\Rightarrow\Delta BDC\) cân tại B
Kẻ đường cao BK \(\Rightarrow KD=KC\)
Xét \(\Delta ABD\) và \(\Delta IBD\) có :
\(\widehat{BAD}=\widehat{BID}\) ( Góc vuông )
\(BD\) cạnh chung
\(\Rightarrow\Delta ABD=\Delta IBD\left(ch-gv\right)\)
\(\Rightarrow AB=DI\) ( 2 cạnh tương ứng )
\(\Leftrightarrow DI=5cm\)
\(DI=CI\Rightarrow CI=5cm\)
\(CD=CI+ID\)
\(\Rightarrow CD=10cm\)
Cho tam giác ABC vuông tại A đường cao AH .Kẻ HM vuông góc AB tại M,HN vuông góc AC tại N. Trên tia đối của tia MH lấy điểm D sao cho MD =MH,trên tia đối của tia NH lấy điểm E sao cho EN =NH. C/m tứ giác BCED là hình thang
1 câu trả lời
Bt1: Hình thang ABCD (góc A= góc D= 90o) có AB= 9cm; CD= 15cm; AC= 17cm. Tính độ dài các cạnh bên.
Bt2: Hình thang ABCD (góc A= góc D= 90o) có AD= 12cm; BC= 13cm; AC= 15cm. Tính độ dài các cạnh đáy.
#Giải hộ..
#Vẽ hình giúp luôn ạ
0 câu trả lời
Bài 4: Cho hình thang ABCD ( AB // CD) có E thuộc cạnh BC sao cho DE là tia phân giác góc D và góc AED = 90 độ . Gọi K là giao điểm của hai đường thẳng AE và DC.
1) C/m tam giác ADK cân ở D.
2) C/m E là trung điểm của BC.
3) Biết AD = 10cm; AE = 6cm. Tính SABCD.
Bài 51: Cho hình thang ABCD ( AB // CD, AB < CD). Kẻ AH vuông góc BD ở H, BK vuông góc AC ở K sao cho AH = BK. C/m:
1) SABC = SBDA.
2) ABCD là hình thang cân.
MIK CẦN GẤP NHÉ!!!
0 câu trả lời
cho tứ giác abcd có góc a =góc d = 90 độ ; AB = 7cm ' AC=20cm;CD=16cm. Tính chu vi hình thang
mong các bạn giúp mình giải thật nhanh
2 câu trả lời
Bài 37: Cho hình thang ABCD (AB // CD) có AB = 13,4cm; AB = 1/3 CD và chiều cao AH bằng trung bình cộng của hai đáy. Tính AH và SABCD.
MiK CẦN GẤP NHÉ!!!
1 câu trả lời
BT: Cho hình thang ABCD có AB//CD
a, Biết ∠B = ∠C.2
Tính ∠B , ∠C
b, ∠B - ∠C = 24o , ∠A = 1,5.∠D
Tính ∠A, ∠B, ∠C, ∠D
1 câu trả lời
a)Ta có: AB // CD => B + C = 180 độ ( Hai góc trong cùng phía)
Thay B = 2C, ta có : 2C + C = 180 => 3C= 180 => C = 60 => B = 60.2 =120
b)Ta có: AB // CD => B + C = 180 độ ( Hai góc trong cùng phía)
Mà B - C = 24 => B = 102 ; C =78
Lại có: A+ D= 180 ( AB//CD; hai góc trong cùng phía)
Mà A = 1.5 D => A= 108; B =72
Cho hình thang ABCD (AB//CD). Biết BC+AD=AB. CMR: các tia phân giác của các góc A và B cắt nhau tại trung điểm của cạnh CD
Được cập nhật 16 tháng 7 lúc 14:22 0 câu trả lời
Cho hình thang cân ABCD , AB // CD biết AB = AB = 2 , AB = BC = 2 , BC = CD = 2 , CD = DA =2 Tính
a,các góc hình thang
b,hai đường chéo
c,độ dài AC
d,diện tích hình thang ABCD
0 câu trả lời
...
Dưới đây là những câu hỏi có bài toán hay do Hoc24 lựa chọn.
Building.
Bảng xếp hạng môn Toán
Nguyễn Huy Tú1835GP
Akai Haruma1799GP
Ace Legona1662GP
Nguyễn Thanh Hằng1072GP
Ribi Nkok Ngok1028GP
Mysterious Person906GP
soyeon_Tiểubàng giải903GP
Võ Đông Anh Tuấn805GP
Phương An797GP
Trần Việt Linh765GP
svtkvtm44GP
Nguyễn Thành Trương39GP
Trần Thanh Phương35GP- tth33GP
- Ngân Vũ Thị30GP
Vũ Huy Hoàng15GP
Dương Bá Gia Bảo14GP
Nguyễn Văn Đạt14GP
Vũ Minh Tuấn14GP
Ťɧε⚡₣lαsɧ13GP
- Nguyễn Thành Trương39GP
- Ngân Vũ Thị30GP
- svtkvtm21GP
- Vũ Minh Tuấn9GP
Aikatstu9GP- lê thị hương giang9GP
- tth9GP
- Dương Bá Gia Bảo8GP
- Ťɧε⚡₣lαsɧ7GP
- Vũ Huy Hoàng6GP
Kết nối hoc24 trên facebook
Có thể bạn quan tâm
Kẻ \(BH\perp CD\) ta được hình chữ nhật ABHD và hình tam giác vuông BHC.
Xét hình chữ nhật ABHD ta có:
\(AB=DH=5\left(cm\right)\)
\(AD=BH=12\left(cm\right)\)
Xét tam giác BHC vuông tại H ta có:
\(BH^2+HC^2=BC^2\) (áp dụng định lý Pytago)
\(\Rightarrow HC^2=BC^2-BH^2=13^2-12^2=169-144=25=5^2\)
\(\Rightarrow HC=5\left(cm\right)\)(do HC>0)
Ta có:
\(DC=DH+HC=5+5=10\left(cm\right)\)
Chúc bạn học tốt!!!