Bài 2: Hình thang

a)xét tam giác NPQ và tam giác HPN có:

góc PNQ=góc HPN =90 độ

góc P chung

\(\Rightarrow\Delta NPQ\infty\Delta HPN\left(g.g\right)\)

b) theo câu a) \(\Delta NPQ\infty\Delta HPN\) nên:

\(\dfrac{NP}{HP}=\dfrac{PQ}{PN}hay\dfrac{15}{HP}=\dfrac{25}{15}\Rightarrow HP=\dfrac{15\cdot15}{25}=\dfrac{225}{25}=9\left(cm\right)\)

HQ=PQ-HP=25-9=16(cm)

bạn tự vẽ hình nha

Xét \(\Delta\)ABD và \(\Delta\)BDC có:

góc ABD=góc BDC(vì AB//CD)

\(\dfrac{AB}{DB}=\dfrac{BD}{DC}=\dfrac{1}{2}\)

\(\Rightarrow\)\(\Delta\)ABD đồng dạng \(\Delta\)BDC(c.g.c)

\(\Rightarrow\)góc A=góc DBC

kẻ AC cắt MN tại I

ta có \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\left(=\dfrac{1}{2}\right)\Rightarrow\)MN//DC//AB(định lí Talet đảo)

ta có:

\(\dfrac{AM}{MD}=\dfrac{1}{2}\Rightarrow\dfrac{AM}{AD}=\dfrac{AM}{AM+MD}=\dfrac{1}{1+2}=\dfrac{1}{3}\\ \Rightarrow\dfrac{BN}{BC}=\dfrac{1}{3}\Rightarrow\dfrac{NC}{BC}=\dfrac{2}{3}\)

tam giác ADC có MI//DC nên :\(\dfrac{MI}{DC}=\dfrac{AM}{AD}\Rightarrow\dfrac{MI}{\left(x+2\right)\left(x-2\right)}=\dfrac{1}{3}\Rightarrow\left(x+2\right)\left(x-2\right)=3MI\)

tam giac CAB có IN//AB nên:

\(\dfrac{NI}{AB}=\dfrac{BN}{BC}\Rightarrow\dfrac{NI}{x+4}=\dfrac{2}{3}\Rightarrow2\left(x+4\right)=3NI\)

\(\left(x+2\right)\left(x-2\right)+2\left(x+4\right)=3MI+3NI\\ \Leftrightarrow x^2-4+2x+8=3\left(MI+NI\right)=3MN=39\\ \Leftrightarrow x^2+2x+4-39=0\\ \Leftrightarrow x^2+2x-35=0\\ \Leftrightarrow\left(x-5\right)\left(x+7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-7\end{matrix}\right.\)

Vậy x=5 hoặc x=-7

a/ Xét tg IAB và tg ICD có :

góc AIB = góc DIC (đói đỉnh )

góc BAI = góc ICD (slt)

=> tg IAB ~ tg ICD (gg)

=> IA/IB=IC/ID

hay IA.ID=IB.IC

\(\Delta ADC\) có DC - AD < AC (bất đẳng thức tam giác)(1)

\(\Delta ABC\) có AC < AB + BC (bất đẳng thức tam giác) (2)

Từ (1) và (2) => DC - AD < AB + BC => DC - AB < AB + BC

Mà AB=2cm CD=5cm => 5 - 2 < AB + BC hay AB + BC > 3 (đpcm)

Xét hình thang ABCD(AB//CD) có : NB=NC; MD=MA

\(\Rightarrow\) MN là đường trung bình hình thang ABCD

\(\Rightarrow\) MN//AB(1)

Ta có: \(\bigtriangleup\)BCA có NB=NC; PC=PA

\(\Rightarrow\) NP là đường trung bình của \(\bigtriangleup\)BCA

\(\Rightarrow\) NP//CD \(\Rightarrow\) NP//AB(vì AB//CD)(2)

Ta có: \(\bigtriangleup\)CDA có MD=MA; PC=PA

\(\Rightarrow\) MP là đường trung bình của \(\bigtriangleup\)CDA

\(\Rightarrow\) MP//CD \(\Rightarrow\) MP//AB(3)

Từ(1);(2);(3)\(\Rightarrow\) M,N,P thẳng hàng(*)

Ta có: \(\bigtriangleup\)CDB có QD=QB;NC=NB

\(\Rightarrow\) NQ là đường trung bình của \(\bigtriangleup\)CDB

\(\Rightarrow\) NQ//CD \(\Rightarrow\) NQ//AB(4)

Ta có: \(\bigtriangleup\)ADB có QD=QB;MD=MA

\(\Rightarrow\) MQ là đường trung bình của \(\bigtriangleup\)ADB

\(\Rightarrow\) MQ//CD \(\Rightarrow\) MQ//AB(4)

Từ(1)(3)(4) \(\Rightarrow\) N,Q,M thẳng hàng(**)

Từ(*);(**) \(\Rightarrow\) N,Q,P,M thẳng hàng

b. Ta có: NM là đường trung bình hình thang ABCD

\(\Rightarrow\) \(MN=\dfrac{x+y}{2}\)

Ta có NQ và MP là đưởng trung bình của \(\bigtriangleup\)CDB và \(\bigtriangleup\)CDA

\(\Rightarrow\) NQ=MP=\(\dfrac{y}{2}\)

Ta lại có: NQ+QP+PM=MN=\(\dfrac{x+y}{2}\)

Hay y + QP=\(\dfrac{x+y}{2}\)

\(\Leftrightarrow\) QP = \(\dfrac{x+y}{2}-y=\dfrac{x+y-2y}{2}=\dfrac{x-y}{2}\)

\(\Rightarrow\) MN+QP=\(\dfrac{x+y}{2}+\dfrac{x-y}{2}=\dfrac{x+y+x-y}{2}=\dfrac{2x}{2}=x\)

c) Ta có: MP=PQ=QN

\(\Leftrightarrow\) \(\dfrac{y}{2}=\dfrac{x-y}{2}=\dfrac{y}{2}\)

\(\Leftrightarrow\) \(\dfrac{y}{2}=\dfrac{x-y+y}{2+2}\) (Tính chất dãy tỉ số bằng nhau)

\(\Leftrightarrow\) \(\dfrac{y}{2}=\dfrac{x}{4}\) \(\Leftrightarrow\) \(4y=2x\) \(\Leftrightarrow\) \(x=2y\)

Bài giải:

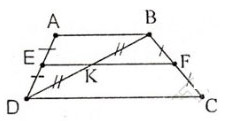
Ta có EA = ED, KB = KD (gt)

Nên EK // AB

Lại có FB = FC, KB = KD (gt)

Nên KF // DC // AB

Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.

Chúc bạn học tốt!

a) Vẽ \(CH\perp AB\)

Tứ giác \(ABCH\) có 3 góc vuông

\(\Rightarrow\) Tứ giác \(ABCH\) là hình chữ nhật

Lại có \(AB=BC\left(gt\right)\)

\(\Rightarrow\widehat{BCH}=90^o\)

\(\Rightarrow BC=AH=CH\)

Ta có:

\(BC=\dfrac{1}{2}AD\left(gt\right)\)

\(\Rightarrow AD=2\cdot BC\)

\(AD=AH+HD\)

\(AD=BC+HD\)

\(2\cdot BC=BC+HD\)

\(\Rightarrow HD=BC\)

Ta có \(CH=BC\) và \(HD=BC\) nên \(CH=HD\)

Xét \(\Delta CHD\) có:

\(CH=HD\)

\(\widehat{CHD}=90^o\)(kề bù với \(\widehat{CHA}\))

\(\Rightarrow\Delta CHD\) vuông cân tại \(H\)

\(\Rightarrow\widehat{HCD}=\widehat{D}=45^o\)

\(\widehat{BDC}=\widehat{BCH}+\widehat{HCD}=90^o+45^o=135^o\)

Vậy \(\widehat{A}=90^o,\widehat{B}=90^o,\widehat{C}=135^o,\widehat{D}=45^o\)

b)

Xét \(\Delta CHA\) có:

\(CH=HA\)

\(\widehat{CHD}=90^o\)

\(\Rightarrow\Delta CHA\) vuông cân tại \(H\)

\(\Rightarrow\widehat{HCA}=\widehat{A}=45^o\)

\(\widehat{ACD}=\widehat{ACH}+\widehat{HCD}=45^o+45^o=90^o\)

\(\Rightarrow AC\perp CD\)

Vậy \(AC\perp CD\)

c)

\(BC=AB=3cm\left(gt\right)\)

\(AD=2\cdot BC=2\cdot3cm=6cm\)

\(HD=BC=3cm\)

Xét \(\Delta CHD\):

Áp dụng định lý Pi-ta-go ta có:

\(HD^2+BC^2=CD^2\\ 3^2+3^2=CD^2\\ CD^2=18\\ CD=\sqrt{18}\left(cm\right)\)

Chu vi hình thang là:

\(3+3+\sqrt{18}+6=12+\sqrt{18}\left(cm\right)\)

Hỏi đáp 24/7 – Giải bài tập cùng Thủ Khoa | Zuni.vn