Bài giải:
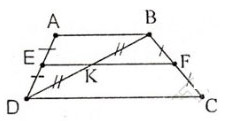
Ta có EA = ED, KB = KD (gt)
Nên EK // AB
Lại có FB = FC, KB = KD (gt)
Nên KF // DC // AB
Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.
Chúc bạn học tốt!![]()
Bài giải:

Ta có EA = ED, KB = KD (gt)
Nên EK // AB
Lại có FB = FC, KB = KD (gt)
Nên KF // DC // AB
Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.
Chúc bạn học tốt!![]()
Cho hình thang ABCD (AB//CD) gọi E , F , K lần lượt là trung điểm của Ad , AC , BC a) Chứng minh EF//CD b) Chứng minh EK//CD c) Chứng minh ba điểm E,F,K thẳng hàng
Cho hình thang ABCD có (AB//CD). Gọi E, F, I lần lượt là trung điểm AD, BC, AC. Chứng minh 3 điểm E, I, F thẳng hàng
Cho hình thang ABCD có AB song song với CD Gọi E , F , I , K lần lượt là trung điểm của AB CD BC AC BD tính EI , IF , EF , EK biết AB = 8 cm CD = 6 cm
cho hình thang ABCD có AB song song CD ( AB< CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.
a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.
b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC = KD.
Cho hình thang ABCD (AB // CD).Gọi E,F lần lượt là trung điểm của AD BC. Biết AB= 6cm, DC= 9cm. Tính độ dài đoạn EF
Cho hình thang ABCD (AB // CD).Gọi E,F lần lượt là trung điểm của AD BC. Biết AB= 6cm, DC= 9cm. Tính độ dài đoạn EF
cho hình thang ABCD(AB//CD)AB<CD GỌI I,K,E lần lượt là trung điểm của BD,AC,BC Chứng minh rằng
a) ba điểm I,k,E thẳng hàng
b) IK= ( CD - AB ):2
vẽ hình hộ mình luôn nha
Cho hình thang ABCD (AB // CD; AB < DC). Gọi D; E; F; G lần lượt là trung điểm của AD; BD; AC vả BC. C/minh:
a, D; E; F; G thẳng hàng
b, \(EF=\dfrac{CD-AB}{2}\)
Bài 4 (3,0 điểm) Cho ∆ABC cân tại A. Gọi M và N lần lượt là trung điểm của cạnh AB và cạnh AC.
1) Chứng minh BC = 2MN.
2) Chứng minh tứ giác MNCB là hình thang cân.
3) Gọi I, K lần lượt là trung điểm của MN và BC. O là giao điểm của MC và NB. Chứng minh: A, I, O, K thẳng hàng.