Phân tích vế trái, ta có:
\(\left(x+y\right)\left(x-y\right)\Leftrightarrow x^2-xy+xy-y^2\Leftrightarrow x^2-y^2\)
Ta thấy vế trái = vế phải => đccm
vì (x+y)*(x-y)=x^2-xy+yx-y^2=x^2-y^2
1. x/y-2=3/2 và x-y=4
2. x-4/y+2=1/2 và x+y=5
3. 3/x-2=2/y+2 và x+y=5
4.3/x-2=2/y+2 và x+y=1
5.x+2/y+3=5/6 và x-y=1
6. x-1/y+4=3/4 và 2x=3y
7. x-1/y+4=3/4 và 2x=3y+2
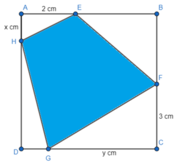
Cho một tấm nhôm hình vuông cạnh 6cm. Người ta muốn cắt một hình thang như hình vẽ. Trong đó A E = 2 ( c m ) , A H = x ( c m ) , C F = 3 ( c m ) , C G = y ( c m ) . Tìm tổng x+y để diện tích hình thang đạt giá trị nhỏ nhất
A.x+y=7
B.x+y=5
C. x + y = 7 2 2
D. x + y = 4 2
Cho x,y,z,t EN .Cm rằng x/(x+y+z)+y/(x+y+t)+z/(y+z+t)+t/(z+t+x) có giá trị không phải số tự nhiên
CHO x;y thuộc Z và x;y khác 0
thỏa mãn \(\frac{x^2}{y^2}+\frac{y^2}{x^2}+2\left(x+y\right)-3\left(\frac{x}{y}+\frac{y}{x}\right)+3\left(\frac{1}{x}+\frac{1}{y}\right)-\frac{2}{xy}=4\)
TÍNH E=x+y
Một sợi dây kim loại dài 32 cm được cắt thành hai đoạn bằng nhau. Đoạn thứ nhất uốn thành một hình chữ nhật có chiều dài 6cm, chiều rộng 2 cm. Đoạn thứ hai uốn thành một tam giác có độ dài một cạnh bằng 6cm. Gọi độ dài hai cạnh còn lại của tam giác là x(cm), y(cm) x ≤ y . Hỏi có bao nhiêu cách chọn bộ số (x;y) sao cho diện tích của tam giác không nhỏ hơn diện tích hình chữ nhật?
A. 0 cách
B. 1 cách
C. 2 cách
D. Vô số cách
Tìm x;y;z biết x/(y+z+1)=y/(x+y+1)=z/(x+y-2)
Chứng minh bất đẳng thức \(\frac{x^2}{y^2}+\frac{y^2}{x^2}+4\ge3\left(\frac{x}{y}+\frac{y}{x}\right)\)
Tính diện tích hình phẳng giới hạn bởi các đường:
a) y = X2, y = x + 2; b) y = |lnx|, y = 1; c) y = (x – 6)2, y = 6x– x2
cho x/2=y/3=z/4 và (x+y)^2 - 4(z-x)^2=9
tìm ba số x, y, z
