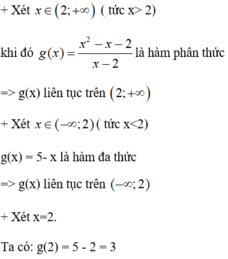
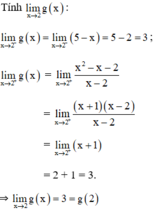
⇒ g(x) liên tục tại 2.
Vậy hàm số g(x) liên tục trên R.
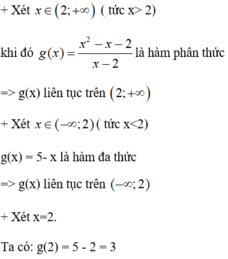
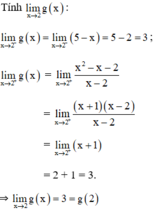
⇒ g(x) liên tục tại 2.
Vậy hàm số g(x) liên tục trên R.
a) Xét tính liên tục của hàm số y = g ( x ) tại x 0 = 2 , biết: g x = x 3 - 8 x - 2 n ế u x ≠ 2 5 n ế u x = 2
b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x 0 = 2 .
xét tính liên tục của hàm số sau trên R
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{2-x}\\x-7\end{matrix}\right.\) khi \(x\ne2\); khi \(x=2\)
Xét tính liên tục của các hàm số sau trên tập xác định của chúng g ( x ) = 1 - x x - 2 2 n ế u x ≠ 2 3 n ế u x = 2
Xét tính liên tục của các hàm số sau trên TXĐ của chúng
f(x)= {x2-3x +4 khi x<2
{ 5 khi x=2
{2x +1 khi x>2
Xét tính liên tục của các hàm số sau trên tập xác định của chúng f ( x ) = x 2 - 2 x - 2 n ế u x ≠ 2 2 2 n ế u x = 2
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x)=x2+sinx;
b) g(x)=x4−x2+\(\dfrac{6}{x-1}\);
c) h(x)=`(2x)/(x−3)+(x−1)/(x+4)`.
xét tính liên tục của hàm số sau tại x = 2
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{2x^2-7x+6}{2-x}\\2x-5\end{matrix}\right.\) khi \(x\ne2\); khi \(x=2\)
Cho hàm số: y = f x = 3 - x 2 + 5 x 2 - 4 x ≠ ± 2 - 1 6 x = 2
- Xét tính liên tục của hàm số f(x) tại x= 2?
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.