\(f\left(x+k\Omega\right)=f\left(x\right)\)
=>Hàm số tuần hoàn theo chu kì \(T=\Omega\)
=>Các hàm số đó là y=tan x, y=cot x; y=sin2x
- Với \(k=2m\left(m\in Z\right)\) hay \(k\) là chẵn
\(y=f\left(x\right)=tanx\Rightarrow f\left(x+k\pi\right)=tan\left(x+2m\pi\right)=tanx=f\left(x\right)\)
\(y=f\left(x\right)=sin2x\Rightarrow f\left(x+k\pi\right)=sin2\left(x+2m\text{ }\pi\right)=sin2x=f\left(x\right)\)
\(y=f\left(x\right)=sinx\Rightarrow f\left(x+k\pi\right)=sin\left(x+2m\pi\right)=sinx=f\left(x\right)\)
\(y=f\left(x\right)=cotx\Rightarrow f\left(x+k\pi\right)=cot\left(x+2m\pi\right)=cotx=f\left(x\right)\)
- Với \(k\) lẻ ta có :
\(y=f\left(x\right)=sin2x\Rightarrow f\left(x+k\pi\right)=sin2\left(x+k\pi\right)=sin2x=f\left(x\right)\)
\(y=f\left(x\right)=sinx\Rightarrow f\left(x+k\pi\right)=sin\left(x+k\pi\right)=-sinx=-f\left(x\right)\)
\(y=f\left(x\right)=tanx\) thỏa mãn \(f\left(x+k\pi\right)=f\left(x\right),\forall x\ne\dfrac{\pi}{2}+k\pi,k\in Z\)
\(y=f\left(x\right)=cotx\) thỏa mãn \(f\left(x+k\pi\right)=f\left(x\right),\forall x\ne k\pi+k\pi,k\in Z\)
Vậy chỉ có hàm số \(y=f\left(x\right)=sin2x\) thỏa tính chất \(f\left(x+k\pi\right)=f\left(x\right),\forall x\in R,k\in Z\)













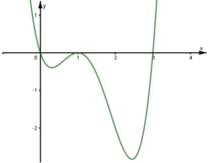
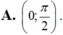
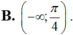
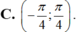
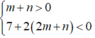 .Tìm số cực trị của hàm số
y
=
f
(
x
)
.Tìm số cực trị của hàm số
y
=
f
(
x
)