Question

mn giúp mình hình 3 4 với 

Answer 1

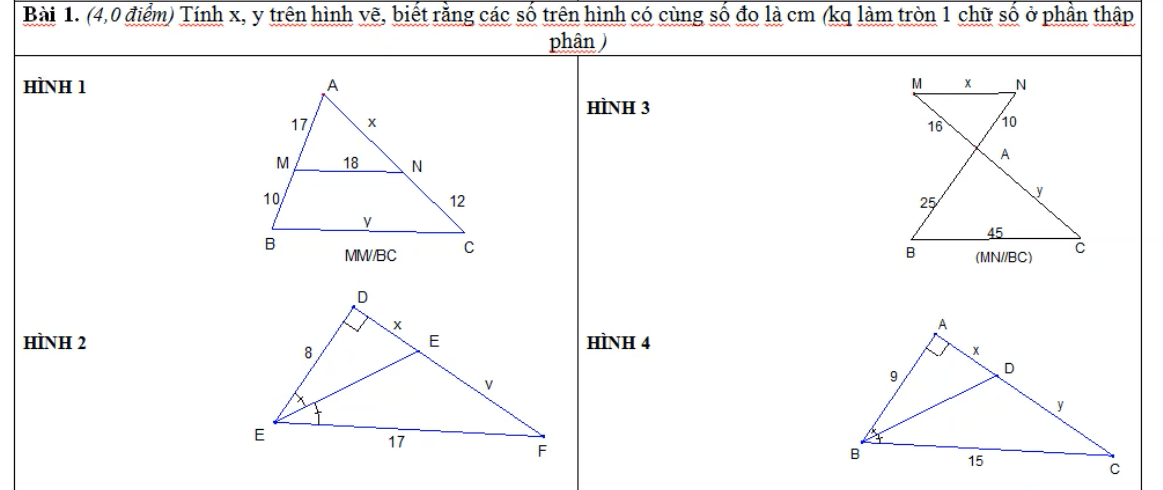
Hình 4: 

\(AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\)

Xét ΔABC cso BD là phân giác

nên x/AB=y/15

=>x/9=y/15

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{9}=\dfrac{y}{15}=\dfrac{x+y}{9+15}=\dfrac{12}{24}=\dfrac{1}{2}\)

Do đó: x=4,5(cm); y=7,5(cm)

Answer 2

Hình 3:

Áp dụng hệ quả của định lý Ta-lét ta có:
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}=\dfrac{MN}{BC}\\ \Rightarrow\dfrac{16}{y}=\dfrac{10}{25}=\dfrac{x}{45}\\ \Rightarrow\left\{{}\begin{matrix}x=18\\y=40\end{matrix}\right.\)

Hình 4:

Áp dụng định lý Pi-ta-go ta có:

\(AB^2+AC^2=BC^2\\ \Rightarrow AC=\sqrt{BC^2-AB^2}\\ \Rightarrow AC=\sqrt{15^2-9^2}\Rightarrow AC=12\)

Áp dụng định lý phân giác ta có:

\(\dfrac{x}{y}=\dfrac{9}{15}\Rightarrow\dfrac{x}{y}=\dfrac{3}{5}\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}\)

Áp dụng t/c dtsbn ta có:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{12}{8}=\dfrac{3}{2}\\ \dfrac{x}{3}=\dfrac{3}{2}\Rightarrow x=4,5\\ \dfrac{y}{5}=\dfrac{3}{2}\Rightarrow y=7,5\)

 

Answer 3

 

4.

Áp dụng định lí pitago, ta có:

\(BC^2=AB^2+AC^2\)

\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{15^2-9^2}=\sqrt{144}=12\)

Ta có:

\(\dfrac{AB}{BC}=\dfrac{AD}{CD}\) ( tính chất đường phân giác góc B )

\(\Rightarrow\dfrac{9}{15}=\dfrac{AD}{CD}\)

\(\Leftrightarrow\dfrac{3}{5}=\dfrac{AD}{CD}\Leftrightarrow\dfrac{CD}{5}=\dfrac{AD}{3}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{CD}{5}=\dfrac{AD}{3}=\dfrac{CD+AD}{5+3}=\dfrac{12}{8}=\dfrac{3}{2}\)

\(\Rightarrow CD=\dfrac{3}{2}.5=7,5\)

\(\Rightarrow CD=\dfrac{3}{2}.3=4,5\)