\(3,=\left(\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\sqrt{xy}\right)\left(\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\right)^2\)
\(=\left[\dfrac{\left(\sqrt{x}\right)^3+\left(\sqrt{y}\right)^3}{\sqrt{x}+\sqrt{y}}-\sqrt{xy}\right]\left[\dfrac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}\right)^2-\left(\sqrt{y}\right)^2}\right]^2\)
\(=\left[\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-\sqrt{xy}\right]\left[\dfrac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}\right]^2\)
\(=\left(x-\sqrt{xy}+y-\sqrt{xy}\right)\left(\dfrac{1}{\sqrt{x}-\sqrt{y}}\right)^2\)
\(=\left(\sqrt{x}-\sqrt{y}\right)^2.\dfrac{1}{\left(\sqrt{x}-\sqrt{y}\right)^2}=1\)
Câu `3` bạn ở trên lm r nhé !
`2)` Với `x >= 0` có:
`[x-\sqrt{3x}+3]/[x\sqrt{x}+3\sqrt{3}]`
`=[x-\sqrt{x}.\sqrt{3}+3]/[(\sqrt{x}+\sqt{3})(x-\sqrt{x}.\sqrt{3}+3)]`
`=1/[\sqrt{x}+\sqrt{3}]`
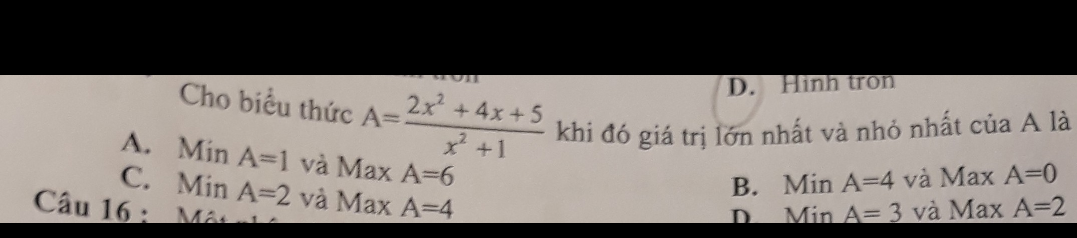
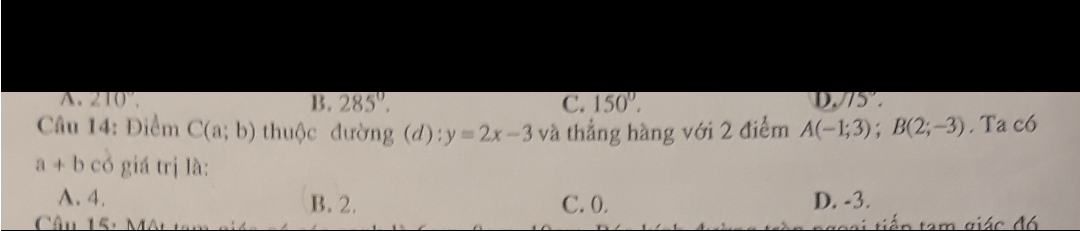
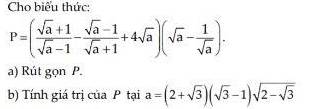
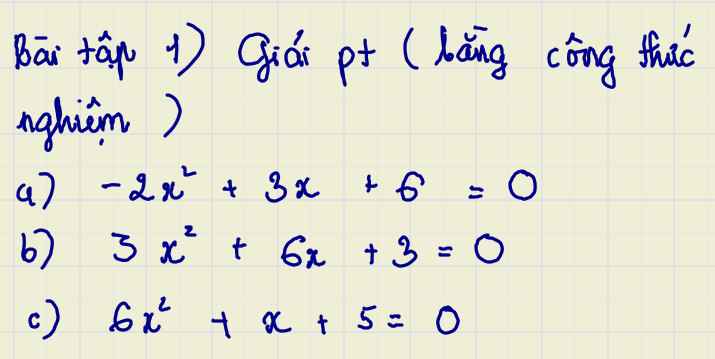
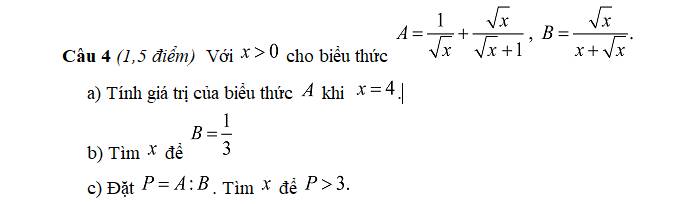
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
