a.
Khi \(x=4\Rightarrow A=\dfrac{1}{\sqrt{4}}+\dfrac{\sqrt{4}}{\sqrt{4}+1}=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\)
b.
\(B=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\sqrt{x}=x+\sqrt{x}\)
\(\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
c.
\(P=A:B=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P>3\Rightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}>3\)
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\) (do \(\sqrt{x}>0\))
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1\ne0\)
\(\Rightarrow x\ne1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)

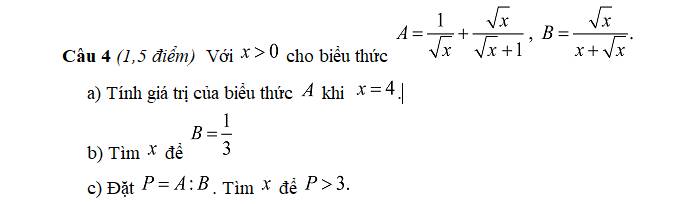




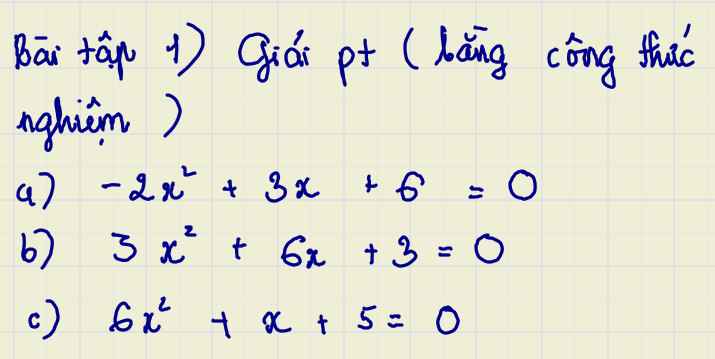



 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn



 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn


