12.
a. Do đường thẳng đi qua điểm A(-5;3) nên ta có:
\(-5a+b=3\) (1)
Do đường thẳng đi qua \(B\left(\dfrac{3}{2};-1\right)\) nên:
\(\dfrac{3}{2}a+b=-1\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}-5a+b=3\\\dfrac{3}{2}a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=-\dfrac{1}{13}\end{matrix}\right.\)
b.
Gọi N là giao điểm (d1) và (d2), tọa độ N là nghiệm:
\(\left\{{}\begin{matrix}2x+5y=17\\4x-10y=14\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\) \(\Rightarrow N\left(6;1\right)\)
Do đường thẳng đi qua M(9;-6) nên:
\(9a+b=-6\)
Do đường thẳng đi qua N(6;1) nên:
\(6a+b=1\)
Ta được hệ: \(\left\{{}\begin{matrix}9a+b=-6\\6a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{7}{3}\\b=15\end{matrix}\right.\)
13.
a.
Hai đường thẳng cắt nhau tại 1 điểm trên trục tung khi hoành độ giao điểm bằng 0
Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ:
\(\left\{{}\begin{matrix}5x-2y=3\\x+y=m\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=3\\2x+2y=2m\end{matrix}\right.\)
\(\Rightarrow7x=2m+3\)
\(\Rightarrow x=\dfrac{2m+3}{7}\)
Hai đường thẳng cắt nhau trên trục tung nên:
\(\dfrac{2m+3}{7}=0\Rightarrow m=-\dfrac{3}{2}\)
Em tự vẽ hình
b.
Hai đường thẳng cắt nhau tại 1 điểm trên trục hoành khi tung độ giao điểm bằng 0.
Tọa độ giao điểm 2 đường thẳng là nghiệm:
\(\left\{{}\begin{matrix}mx+3y=10\\x-2y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}mx+3y=10\\mx-2my=4m\end{matrix}\right.\)
Trừ vế cho vế \(\Rightarrow\left(2m+3\right)y=10-4m\)
2 đường thẳng cắt nhau khi \(2m+3\ne0\Rightarrow m\ne-\dfrac{3}{2}\)
Khi đó tung độ giao điểm là: \(y=\dfrac{10-4m}{2m+3}\)
2 đường cắt nhau trên trục hoành khi:
\(\dfrac{10-4m}{2m+3}=0\Rightarrow10-4m=0\)
\(\Rightarrow m=\dfrac{5}{2}\)
14.
a. Do (d1) đi qua A(5;-1) nên ta có:
\(5.5-2.\left(-1\right)=c\Rightarrow c=27\)
Phương trình (d1): \(5x-2y=27\)
Do (d2) qua B(-7;3) nên:
\(-7+3b=2\Rightarrow b=3\)
Phương trình (d2): \(x+3y=2\)
Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ:
\(\left\{{}\begin{matrix}5x-2y=27\\x+3y=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy giao điểm của 2 đường thẳng có tọa độ \(\left(5;-1\right)\)
b.
Câu này làm giống hệt câu a, em tự giải
Bài 13:
a: (d1): 5x-2y=3
=>2y=5x-3
=>\(y=\dfrac{5}{2}x-\dfrac{3}{2}\)
(d2): x+y=m
=>y=-x+m
Để (d1) cắt (d2) tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}\dfrac{5}{2}\ne-1\\m=-\dfrac{3}{2}\end{matrix}\right.\)
=>\(m=-\dfrac{3}{2}\)
Vậy: (d2): \(y=-x-\dfrac{3}{2}\); (d1): 5x-2y=3
*Vẽ đồ thị:
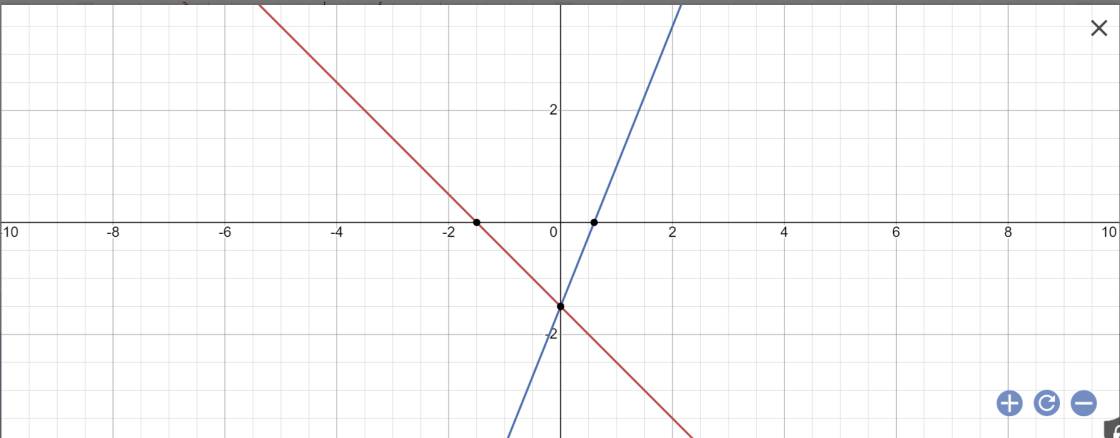
b: (d1): mx+3y=10
=>3y=-mx+10
=>\(y=x\cdot\dfrac{-m}{3}+\dfrac{10}{3}\)
(d2): x-2y=4
=>2y=x-4
=>\(y=\dfrac{1}{2}x-2\)
Để (d1) cắt (d2) tại một điểm trên trục Ox thì \(\left\{{}\begin{matrix}-\dfrac{m}{3}\ne\dfrac{1}{2}\\\dfrac{-10}{3}:\dfrac{-m}{3}=\dfrac{-\left(-2\right)}{\dfrac{1}{2}}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne-\dfrac{3}{2}\\\dfrac{10}{m}=2\cdot2=4\end{matrix}\right.\)
=>m=5/2(nhận)
Thay m=5/2 vào (d1), ta được:
\(\dfrac{5}{2}x+3y=10\)
=>\(3y=10-\dfrac{5}{2}x\)
=>\(y=-\dfrac{5}{6}x+\dfrac{10}{3}\)
(d2): \(y=\dfrac{1}{2}x-2\)
Vẽ đồ thị:
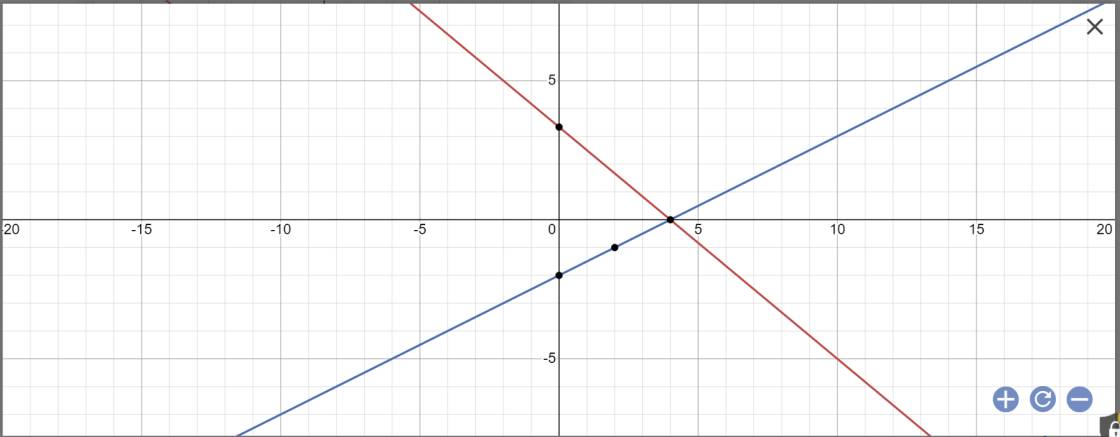
Bài 14:
a: Thay x=5 và y=-1 vào (d1), ta được:
\(5\cdot5-2\cdot\left(-1\right)=c\)
=>c=25+2=27
=>(d1): 5x-2y=27
Thay x=-7 và y=3 vào (d2), ta được:
\(-7+3b=2\)
=>3b=9
=>b=3
=>(d2): x+3y=2
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+3y=2\\5x-2y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x+15y=10\\5x-2y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x+3y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-1\\x=2-3y=2-3\cdot\left(-1\right)=2+3=5\end{matrix}\right.\)
b: Thay x=3 và y=9 vào (d1), ta được:
\(3\cdot a+2\cdot9=-3\)
=>3a+18=-3
=>3a=-21
=>a=-7
Thay x=-1 và y=2 vào (d2), ta được:
\(3\cdot\left(-1\right)-b\cdot2=5\)
=>-2b-3=5
=>-2b=8
=>b=-4
Thay b=-4 vào (d2), ta được:
\(3x-y\cdot\left(-4\right)=5\)
=>3x+4y=5
(d1): -7x+2y=-3
(d2): 3x+4y=5
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}-7x+2y=-3\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-14x+4y=-6\\3x+4y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-17x=-11\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{17}\\4y=5-3x=5-\dfrac{33}{17}=\dfrac{85}{17}-\dfrac{33}{17}=\dfrac{52}{17}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{11}{17}\\y=\dfrac{13}{17}\end{matrix}\right.\)

 cứu e vssss
cứu e vssss
















