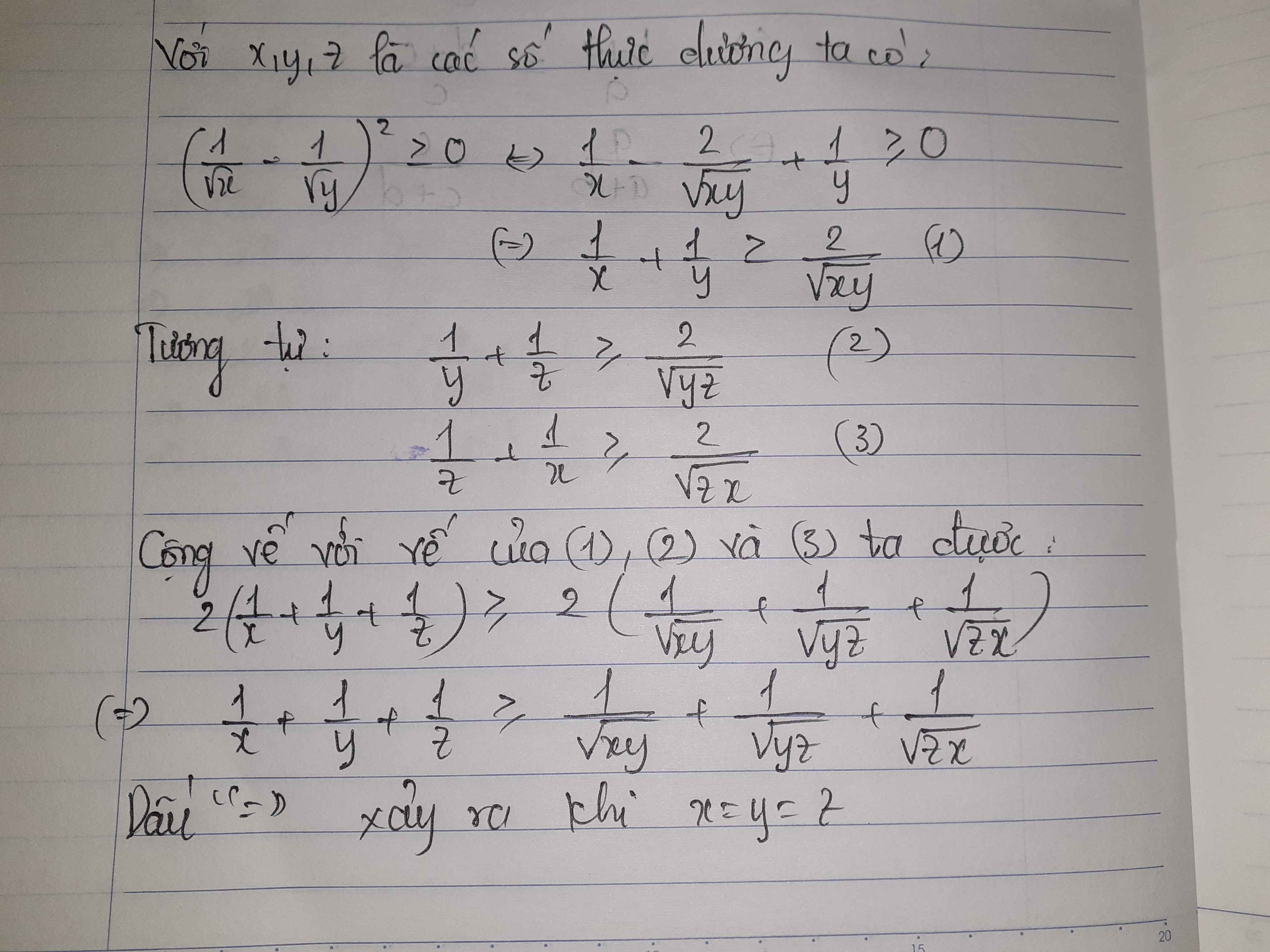\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{1}{\sqrt{xy}}+\dfrac{1}{\sqrt{yz}}+\dfrac{1}{\sqrt{zx}}\)
\(\Rightarrow\dfrac{2}{x}+\dfrac{2}{y}+\dfrac{2}{z}\ge\dfrac{2}{\sqrt{xy}}+\dfrac{2}{\sqrt{yz}}+\dfrac{2}{\sqrt{zx}}\)
\(\Rightarrow\dfrac{2}{x}+\dfrac{2}{y}+\dfrac{2}{z}-\dfrac{2}{\sqrt{xy}}+\dfrac{2}{\sqrt{yz}}+\dfrac{2}{\sqrt{zx}}\ge0\)
\(\Rightarrow\dfrac{1}{x}-\dfrac{2}{\sqrt{xy}}+\dfrac{1}{y}+\dfrac{1}{y}-\dfrac{2}{\sqrt{yz}}+\dfrac{1}{z}+\dfrac{1}{z}-\dfrac{2}{\sqrt{zx}}+\dfrac{1}{x}\ge0\)
\(\Rightarrow\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\right)^2+\left(\dfrac{1}{\sqrt{y}}-\dfrac{1}{\sqrt{z}}\right)^2+\left(\dfrac{1}{\sqrt{z}}-\dfrac{1}{\sqrt{x}}\right)^2\ge0\) (luôn đúng)
Dấu = xảy ra khi \(x=y=z\)