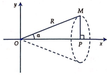
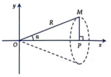
a) Hoành độ điểm P là :
xp = OP = OM. cos α = R.cosα
Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:
b) Đặt t = cosα => t ∈ . (vì α ∈
), α = arccos t.
Ta có :
V' = 0 ⇔
hoặc (loại).
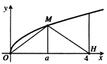
Ta có bảng biến thiên:
Từ đó suy ra V(t) lớn nhất ⇔ , khi đó :
.