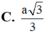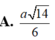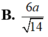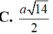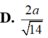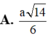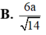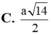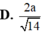Qua M kẻ đường thẳng song song ND cắt AD kéo dài tại E
\(\dfrac{DE}{CN}=\dfrac{DM}{DC}=\dfrac{1}{2}\) (hai tam giác MDE và DCN đồng dạng)
\(\Rightarrow DE=\dfrac{1}{2}CN=\dfrac{a}{4}\Rightarrow AE=\dfrac{5a}{4}=5DE\)
\(\Rightarrow D\left(ND;SM\right)=d\left(D;\left(SME\right)\right)=\dfrac{1}{2}d\left(A;\left(SME\right)\right)\)
\(ME=\sqrt{DE^2+MD^2}=\dfrac{a\sqrt{5}}{4}\)
\(AM=\sqrt{AD^2+DM^2}=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow AM^2+ME^2=\dfrac{25a^2}{16}=AE^2\)
\(\Rightarrow\Delta AME\) vuông tại M \(\Rightarrow ME\perp\left(SAM\right)\)
TỪ A kẻ \(AH\perp SM\Rightarrow AH\perp\left(SME\right)\)
\(\Rightarrow AH=d\left(A;\left(SME\right)\right)\)
\(d\left(ND;SM\right)=\dfrac{1}{5}AH=\dfrac{1}{5}.\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=\)