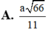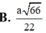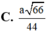Bài này có thể tính gián tiếp như sau:
Cho mặt phẳng (P) và đường thẳng (d) cắt (P)
Gọi \(\left(d'\right)\) là đường thẳng vuông góc với (P) (đường thẳng pháp tuyến). Khi đó góc giữa (d) và (P) sẽ phụ nhau với góc giữa (d) và (d'). Tính chất này có thể chứng minh 1 cách dễ dàng
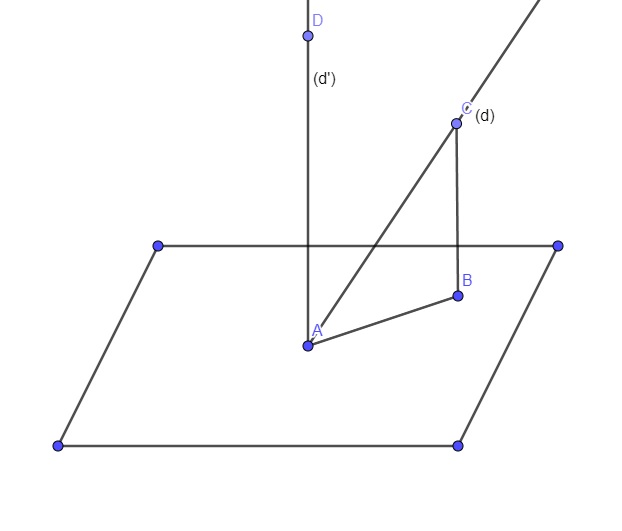
Giả sử AB là hình chiếu vuông góc của (d) lên (P), khi đó góc giữa (d) và (P) là \(\widehat{CAB}\), do (d') vuông góc (P) nên \(\widehat{DAB}=90^0\Rightarrow\widehat{DAC}=90^0-\widehat{CAB}\)
Vậy thay vì phải tìm hình chiếu vuông góc của đường lên mặt, ta tìm 1 đường vuông góc với mặt và cắt đường (d), sau đó tính góc giữa 2 đường rồi lấy 90 độ trừ đi là xong.
Cũng có thể áp dụng các này khi tính góc giữa 2 mặt trong vài trường hợp, nếu khó xác định góc chung thì có thể nghĩ cách tính góc giữa 2 đường pháp tuyến của 2 mặt. Khi đó góc giữa 2 mặt bằng góc giữa 2 đường thẳng pháp tuyến của 2 mặt đó.
Ở bài này, dễ dàng chứng minh \(CD\perp\left(SAC\right)\), vậy ta chỉ cần tính sin góc giữa CD và MN (cắt nhau tại N) là có cosin góc giữa MN và (SAC)