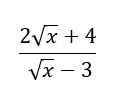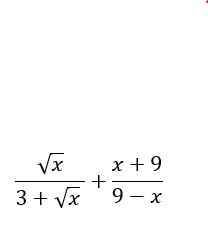Question

Cho hai biểu thức : A=  và B = 

a) Tính giá trị biểu thức A khi x = 4

b) Rút gọn biểu thức B

c) Biết C= B/A. Tìm x nguyên để C < -1/3.

Answer 1

`a)` Với `x=4` (t/m `x >= 0,x \ne 9`). Thay `x=4` vào `A` có:

 `A=[2\sqrt{4}+4]/[\sqrt{4}-3]=[4+4]/[2-3]=-8`

______________________________________________

`b)` Với `x >= 0,x \ne 9` có:

`B=\sqrt{x}/[3+\sqrt{x}]+[x+9]/[9-x]`

`B=[\sqrt{x}(3-\sqrt{x})+x+9]/[(3-\sqrt{x})(3+\sqrt{x})]`

`B=[3\sqrt{x}-x+x+9]/[(3-\sqrt{x})(3+\sqrt{x})]`

`B=[3(\sqrt{x}+3)]/[(3-\sqrt{x})(3+\sqrt{x})]`

`B=3/[3-\sqrt{x}`

_______________________________________

`c)` Với `x >= 0,x \ne 9` có:

`C=B/A=3/[3-\sqrt{x}]:[2\sqrt{x}+4]/[\sqrt{x}-3]`

          `=[-3]/[\sqrt{x}-3].[\sqrt{x}-3]/[2\sqrt{x}+4]`

          `=[-3]/[2\sqrt{x}+4]`

`C < -1/3<=>[-3]/[2\sqrt{x}+4] < -1/3`

             `<=>[-3]/[2\sqrt{x}+4]+1/3 < 0`

             `<=>[-9+2\sqrt{x}+4]/[6\sqrt{x}+12] < 0`

             `<=>[2\sqrt{x}-5]/[6\sqrt{x}+12] < 0`

      Với `x >= 0=>6\sqrt{x}+12 > 0`

   `=>2\sqrt{x}-5 < 0`

`<=>\sqrt{x} < 5/2`

`<=>x < 25/4`  Kết hợp đk

  `=>0 <= x < 25/4`

  Mà `x in ZZ`

 `=>x in {0;1;2;3;4;5;6}`

Answer 2

a)

$A = \dfrac{ 2\sqrt{4} + 4}{ \sqrt{4} -3} = -8$

b)

$B = \dfrac{ \sqrt{x} }{3 + \sqrt{x}} + \sqrt{ x+ 9}{ (3 + \sqrt{x})(3 - \sqrt{x})}$
$= \dfrac{ \sqrt{x}( 3 - \sqrt{x}) + x + 9}{ 9 - x}$
$= \dfrac{ 3 \sqrt{x} + 9}{9 - x}$
$= \dfrac{3}{3 - \sqrt{x}}$

c)

$C = \dfrac{3}{3 - \sqrt{x}} : \dfrac{2 \sqrt{x} + 4}{\sqrt{x} - 3}$

$= \dfrac{3}{3 - \sqrt{x}} . \dfrac{ \sqrt{x} -3}{ 2 \sqrt{x} + 4}$
$= \dfrac{-3}{2 \sqrt{x} + 4} < \dfrac{-1}{3}$

$\Rightarrow \dfrac{3}{2 \sqrt{x} + 4} > \dfrac{1}{3}$

$⇔ \dfrac{3}{2 \sqrt{x} + 4} - \dfrac{1}{3}  > 0$
$⇔\dfrac{9 - 2\sqrt{x} - 4}{3( 2\sqrt{x} + 4)} > 0$
$⇔ 5 - 2\sqrt{x} > 0$

$⇔ \sqrt{x} < \dfrac{5}{2}$

$⇔ x < \dfrac{25}{4}$

Suy ra : $0 < x < \dfrac{25}{4}$