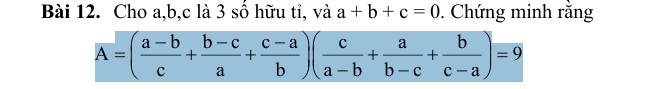Question

Bài 12. Cho a, b, c là 3 số hữu tỉ, và \( a + b + c = 0 \). Chứng minh rằng
\[
A = \left( \frac{a-b}{c} + \frac{b-c}{a} + \frac{c-a}{b} \right) \left( \frac{c}{a-b} + \frac{a}{b-c} + \frac{b}{c-a} \right) = 9
\]

Answer 1

a+b+c=0 => a= -c-b

                     b= -c-a

                      c = -b-a

thay vào : a-b/-b-a  + b-c/-c-b  + c - a / -c-a = -1 - 1-1 = -3 

thay vào vế phải tương tự ta được -3 => A = -3 nhân -3 = 9

Answer 2

Đặt \(\dfrac{a-b}{c}=x\Rightarrow\dfrac{1}{x}=\dfrac{c}{a-b}\)

\(\dfrac{b-c}{a}=y\Rightarrow\dfrac{1}{y}=\dfrac{a}{b-c}\)

\(\dfrac{c-a}{b}=z\Rightarrow\dfrac{1}{z}=\dfrac{b}{c-a}\)

\(\Rightarrow A=\left(x+y+z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)

Áp dụng Bđt Cauchy ta có :

\(x+y+z\ge3\sqrt[3]{xyz}\)

\(\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\ge3\sqrt[3]{\dfrac{1}{xyz}}\)

\(\Rightarrow A=\left(x+y+z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\ge3.3.\sqrt[3]{xyz.\dfrac{1}{xyz}}=9\)

Dấu "=" xảy ra khi \(x=y=z\)

\(\Rightarrow\dfrac{a-b}{c}=\dfrac{b-c}{a}=\dfrac{c-a}{b}=\dfrac{a-b+b-c+c-a}{a+b+c}=0\)

\(\Rightarrow a=b=c=0\) (Đúng với \(a+b+c=0\))

Vậy ta được đpcm