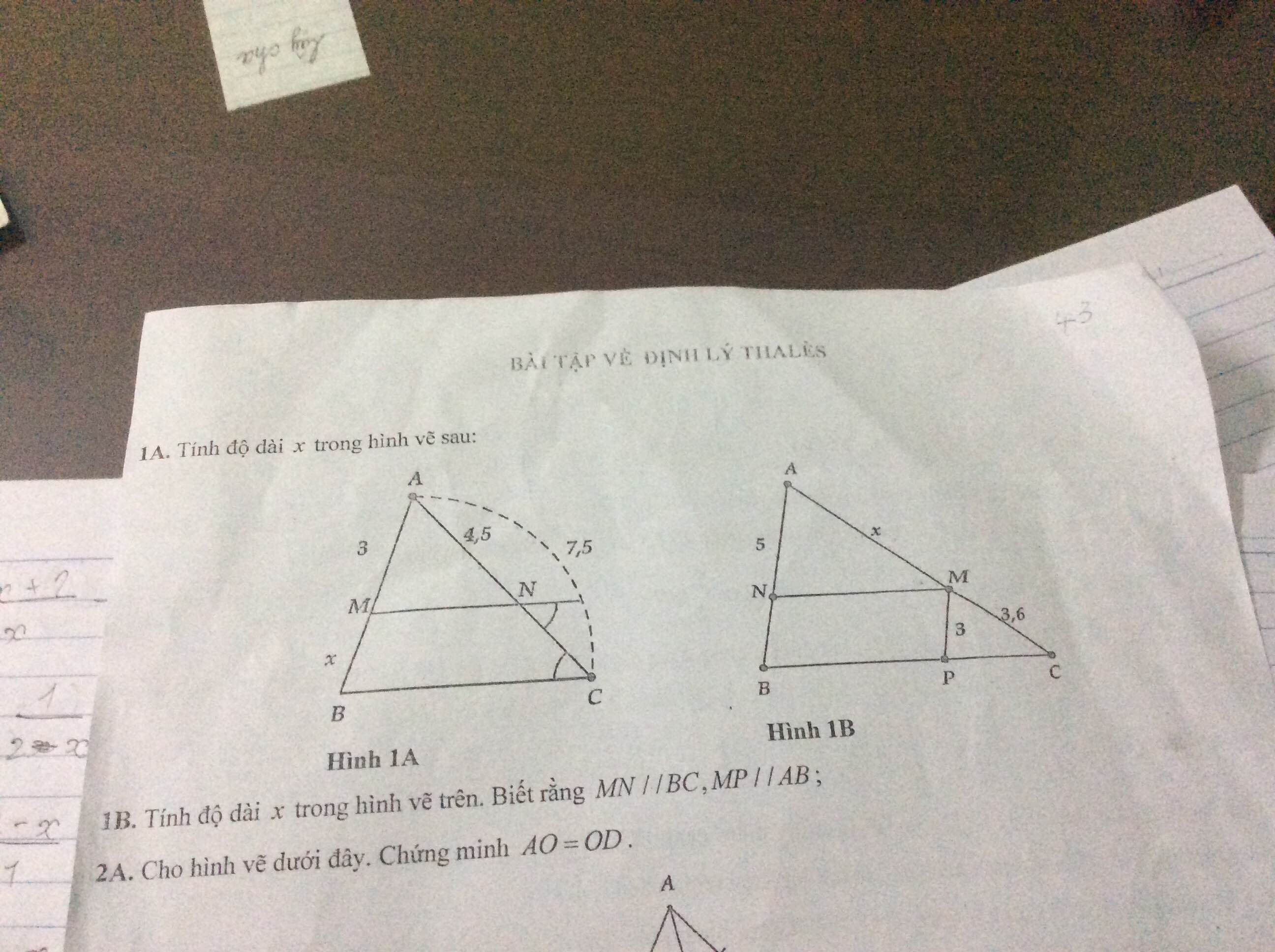
Xét `ΔABC` có: `MN` // `BC `
Áp dụng định lý talet cho `ΔABC`
`=> (AM)/(AB) = (AN)/(AC) `
`=> 3/(AB) = (4,5)/(7,5) `
`=> AB = 5 `
`=> MB = 5-3 = 2`
---------------------------
Tứ giác `NMPB` có: `NB` // `MP; NM` // `BP`
`=>` Tứ giác `NMPB` là hình bình hành
`=> NB = MP`
`=> NP = 3`
`=> AB = 5+3 = 8`
Xét `ΔABC` có: `MP`//`AB`
Áp dụng định lý Talet cho `ΔABC`
`=> (MC)/(AC) = (MP)/(AB)`
`=> (3,6)/(AC) = 3/8`
`=> AC = 9,6`
`=> AM = 9,6 - 3,6 = 6`
1A: Vì có hai góc so le trong bằng nhau nên MN//BC
AN+NC=AC
=>NC+4,5=7,5
=>NC=3
Xét ΔABC có MN//BC
nên \(\dfrac{AN}{NC}=\dfrac{AM}{MB}\)
=>\(\dfrac{3}{x}=\dfrac{4.5}{3}=\dfrac{3}{2}\)
=>x=2
1B
Xét tứ giác MNBP có
MN//BP
MP//BN
Do đó: MNBP là hình bình hành
=>MP=NB
=>NB=3
AB=AN+NB=5+3=8
Xét ΔABC có MN//BC
nên \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)
=>\(\dfrac{5}{8}=\dfrac{x}{x+3,6}\)
=>8x=5x+18
=>3x=18
=>x=6