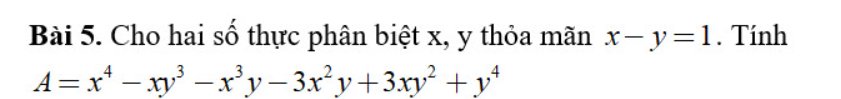\(A=x^4-xy^3-x^3y-3x^2y+3xy^2+y^4\\ =\left(x^4-x^3y\right)-\left(xy^3-y^4\right)-\left(3x^2y-3xy^2\right)\\ =x^3\left(x-y\right)-y^3\left(x-y\right)-3xy\left(x-y\right)\\ =x^3-y^3-3xy\\ =\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\\ =x^2+xy+y^2-3xy\\ =x^2-2xy+y^2\\ =\left(x-y\right)^2\\ =1^2=1\)
A = x⁴ − xy³ − x³y − 3x²y + 3xy² + y⁴
= (x⁴ − x³y) + (−xy³ + y⁴) + (−3x²y + 3xy²)
= x³(x − y) − y³(x − y) − 3xy(x − y)
= (x − y)(x³ − y³ − 3xy)
= (x − y)[(x³ − y³) − 3xy]
= (x − y)[(x − y)(x² + xy + y²) − 3xy]
= 1.[1.(x² + xy + y²) − 3xy]
= x² + xy + y² − 3xy
= x² − 2xy + y²
= (x − y)²
= 1²
= 1