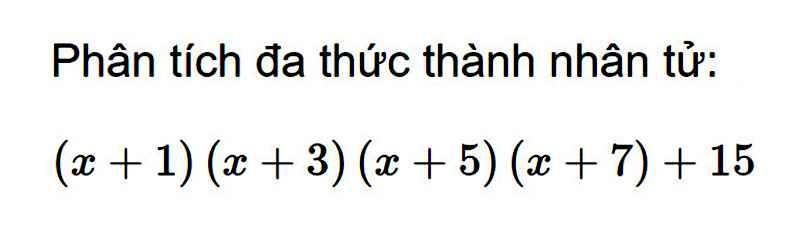Question

 

Answer 1

`(x+1)(x+3)(x+5)(x+7)+15`

`=(x+1)(x+7)(x+3)(x+5)+15`

`= (x^2+7x+x+7)(x^2+5x+3x+15)+15 `

`=(x^2 +8x+7)(x^2+8x+15)+15`

Đặt `t=x^2 +8x+11`

`=(t-4)(t+4)+15`

`=t^2 -16 +15`

`=t^2 -1`

`=(t-1)(t+1)`

`=(x^2 +8x+11-1)(x^2 +8x+11+1)`

`=(x^2 +8x+10)(x^2 +8x+12)`

Answer 2

Answer 3

\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)

\(=\left(x+1\right)\left(x+7\right)\left(x+3\right)\left(x+5\right)+15\)

\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)

\(=\left(x^2+8x\right)^2+22\left(x^2+8x\right)+120\)

\(=\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)

\(=\left(x^2+8x+10\right)\left(x+2\right)\left(x+6\right)\)