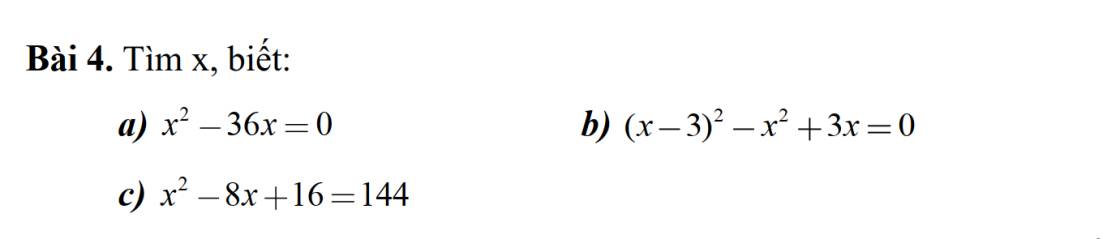a: \(x^2-36x=0\)
=>\(x\cdot x-x\cdot36=0\)
=>\(x\left(x-36\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-36=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=36\end{matrix}\right.\)
b: \(\left(x-3\right)^2-x^2+3x=0\)
=>\(x^2-6x+9-x^2+3x=0\)
=>-3x+9=0
=>-3x=-9
=>x=3
c: \(x^2-8x+16=144\)
=>\(x^2-2\cdot x\cdot4+4^2=144\)
=>\(\left(x-4\right)^2=144\)
=>\(\left[{}\begin{matrix}x-4=12\\x-4=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-8\end{matrix}\right.\)
a) \(x^2-36x=0\)
\(\Leftrightarrow x\left(x-36\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-36=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=36\end{matrix}\right.\)
b) \(\left(x-3\right)^2-x^2+3x=0\)
\(\Leftrightarrow\left(x-3\right)^2-x\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-3-x\right)=0\)
\(\Leftrightarrow-3\left(x-3\right)=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
c) \(x^2-8x+16=144\)
\(\Leftrightarrow x^2-2\cdot x\cdot4+4^2=\left(\pm12\right)^2\)
\(\Leftrightarrow\left(x-4\right)^2=\left(\pm12\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=12\\x-4=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-8\end{matrix}\right.\)
a) x² - 36x = 0
x.(x - 36) = 0
x = 0 hoặc x - 36 = 0
*) x - 36 = 0
x = 0 + 36
x = 36
Vậy x = 0; x = 36
b) (x - 3)² - x² + 3x = 0
(x - )² - (x² - 3x) = 0
(x - 3)² - x(x - 3) = 0
(x - 3)(x - 3 - x) = 0
(x - 3).(-3) = 0
x - 3 = 0
x = 0 + 3
x = 3
c) x² - 8x + 16 = 144
(x - 4)² = 144
x - 4 = 12 hoặc x - 4 = -12
*) x - 4 = 12
x = 12 + 4
x = 16
*) x - 4 = -12
x = -12 + 4
x = -8
Vậy x = -8; x = 16