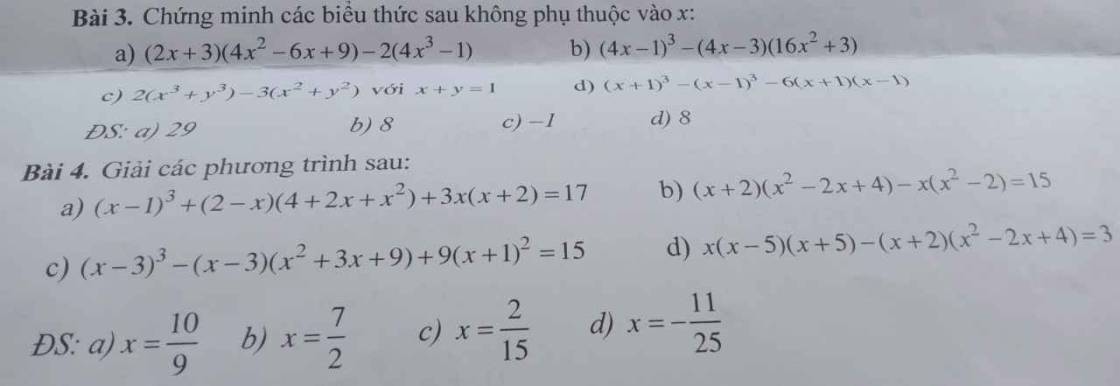Bạn cần giúp bài nào ạ? Tách các bài ra từng CH khác nhau nếu cần tất cả.
Bài 3:
a) \(\left(2x+3\right)\left(4x^2-6x+9\right)-2\left(4x^3-1\right)\)
\(=\left(2x\right)^3+3^3-2\left(4x^3-1\right)\)
\(=8x^3+27-8x^3+2\)
\(=29\)
Vậy giá trị của biểu thức không phụ thuộc vào biến
b) \(\left(4x-1\right)^3-\left(4x-3\right)\left(16x^2+3\right)\)
\(=\left(4x\right)^3-3\cdot\left(4x\right)^2\cdot1+3\cdot4x\cdot1^2-1^3-\left(64x^3+12x-48x^2-9\right)\)
\(=64x^3-48x^2+12x-1-64x^3-12x+48x^2+9\)
\(=8\)
Vậy giá trị của biểu thức không phụ thuộc vào biến
c) \(2\left(x^3+y^3\right)-3\left(x^2+y^2\right)\)
\(=2\left(x+y\right)\left(x^2-xy+y^2\right)-3\left(x^2+y^2\right)\)
\(=2\left(x^2-xy+y^2\right)-3\left(x^2+y^2\right)\)
\(=2x^2-2xy+y^2-3x^2-3y^2\)
\(=-x^2-2xy-y^2\)
\(=-\left(x+y\right)^2\)
\(=-\left(1\right)^2\)
\(=-1\)
Vậy giá trị của biểu thức không phụ thuộc vào biến
d) \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x+1\right)\left(x-1\right)\)
\(=x^3+3x^2+3x+1-\left(x^3-3x^2+3x-1\right)-6\left(x^2-1\right)\)
\(=x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+6\)
\(=8\)
Vậy giá trị của biểu thức không phụ thuộc vào biến
4:
a: \(\left(x-1\right)^3+\left(2-x\right)\left(4+2x+x^2\right)+3x\left(x+2\right)=17\)
=>\(x^3-3x^2+3x-1+8-x^3+3x\left(x+2\right)=17\)
=>\(-3x^2+3x+7+3x^2+6x=17\)
=>9x=10
=>x=10/9
b: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2-2\right)=15\)
=>\(x^3+8-x^3+2x=15\)
=>2x+8=15
=>2x=7
=>x=7/2
c: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=15\)
=>\(x^3-9x^2+27x-27-x^3+27+9\left(x^2+2x+1\right)=15\)
=>\(-9x^2+27x+9x^2+18x+9=15\)
=>45x=6
=>\(x=\dfrac{2}{15}\)
d: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=3\)
=>\(x\left(x^2-25\right)-x^3-8=3\)
=>\(x^3-25x-x^3-8=3\)
=>\(-25x=11\)
=>\(x=-\dfrac{11}{25}\)