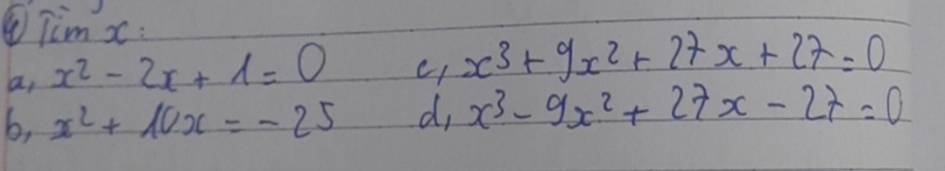\(a,x^2-2x+1=0\\\Leftrightarrow (x-1)^2=0\\\Leftrightarrow x-1=0\\\Leftrightarrow x=1\\---\\b,x^2+10x=-25\\\Leftrightarrow x^2+10x+25=0\\\Leftrightarrow x^2+2\cdot x\cdot5+5^2=0\\\Leftrightarrow(x+5)^2=0\\\Leftrightarrow x+5=0\\\Leftrightarrow x=-5\\---\)
\(c,x^3+9x^2+27x+27=0\\\Leftrightarrow x^3+3\cdot x^2\cdot3+3\cdot x\cdot3^2+3^3=0\\\Leftrightarrow(x+3)^3=0\\\Leftrightarrow x+3=0\\\Leftrightarrow x=-3\\---\\d,x^3-9x^2+27x-27=0\\\Leftrightarrow x^3-3\cdot x^2\cdot3 +3\cdot x\cdot3^2-3^3=0\\\Leftrightarrow(x-3)^3=0\\\Leftrightarrow x-3=0\\\Leftrightarrow x=3\\Toru\)
`#3107.101107`
4.
a,
`x^2 - 2x + 1 = 0`
`<=> (x - 1)^2 = 0`
`<=> x - 1 = 0`
`<=> x = 1`
Vậy, `x = 1`
b,
`x^3 +9x^2 +27x + 27 = 0`
`<=> (x + 3)^3 = 0`
`<=> x + 3 = 0`
`<=> x = -3`
Vậy, `x = -3`
c,
`x^2 + 10x = -25`
`<=> x^2 + 10x + 25 = 0`
`<=> x^2 + 2*x*5 + 5^2 = 0`
`<=> (x + 5)^2 = 0`
`<=> x + 5 = 0`
`<=> x = -5`
Vậy, `x = -5`
d,
`x^3 - 9x^2 + 27x - 27 = 0`
`<=> x^3 - 3*x^2*3 + 3*x*3^2 - 3^3 = 0`
`<=> (x - 3)^3 = 0`
`<=> x - 3 = 0`
`<=> x = 3`
Vậy, `x = 3.`
____
Sử dụng hđt:
1) \(\left(A+B\right)^2=A^2+2AB+B^2\)
2)\(\left(A-B\right)^2=A^2-2AB+B^2\)
3) \(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
4) \(\left(A-B\right)^3=A^3-3A^2B+3AB^2-B^3\)
a: \(x^2-2x+1=0\)
=>\(\left(x-1\right)^2=0\)
=>x-1=0
=>x=1
b: \(x^2+10x=-25\)
=>\(x^2+10x+25=0\)
=>\(\left(x+5\right)^2=0\)
=>x+5=0
=>x=-5
c: \(x^3+9x^2+27x+27=0\)
=>\(x^3+3\cdot x^2\cdot3+3\cdot x\cdot3^2+3^3=0\)
=>\(\left(x+3\right)^3=0\)
=>x+3=0
=>x=-3
d: \(x^3-9x^2+27x-27=0\)
=>\(x^3-3\cdot x^2\cdot3+3\cdot x\cdot3^2-3^3=0\)
=>\(\left(x-3\right)^3=0\)
=>x-3=0
=>x=3