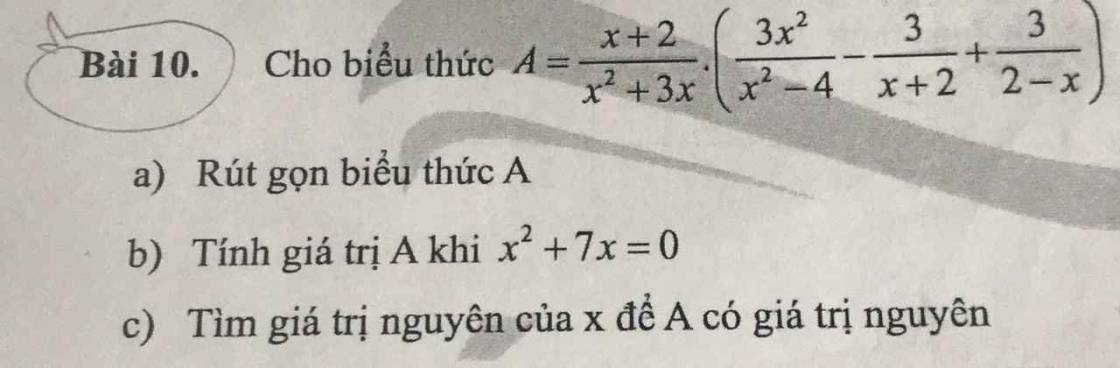a) \(A=\dfrac{x+2}{x^2+3x}\cdot\left(\dfrac{3x^2}{x^2-4}-\dfrac{3}{x+2}+\dfrac{3}{2-x}\right)\) (ĐKXĐ: \(x\ne0;x\ne-3;x\ne\pm2\))
\(=\dfrac{x+2}{x^2+3x}\cdot\left(\dfrac{3x^2}{x^2-4}-\dfrac{3}{x+2}-\dfrac{3}{x-2}\right)\)
\(=\dfrac{x+2}{x^2+3x}\cdot\left[\dfrac{3x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=\dfrac{x+2}{x\left(x+3\right)}\cdot\dfrac{3x^2-3x+6-3x-6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3x^2-6x}{x\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{3x\left(x-2\right)}{x\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{3}{x+3}\)
\(---\)
b) Có: \(x^2+7x=0\)
\(\Leftrightarrow x\left(x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-7\left(tm\right)\end{matrix}\right.\)
Với \(x=-7\), A trở thành:
\(A=\dfrac{3}{-7+3}=-\dfrac{3}{4}\)
\(---\)
c) Để \(A\) có giá trị nguyên thì \(\dfrac{3}{x+3}\) có giá trị nguyên
\(\Rightarrow x+3\inƯ\left(3\right)\)
\(\Rightarrow x+3\in\left\{1;3;-1;-3\right\}\)
\(\Rightarrow x\in\left\{-2;0;-4;-6\right\}\)
Kết hợp với điều kiện xác định của x, ta được:
\(x\in\left\{-4;-6\right\}\)
Vậy: ...
\(Toru\)