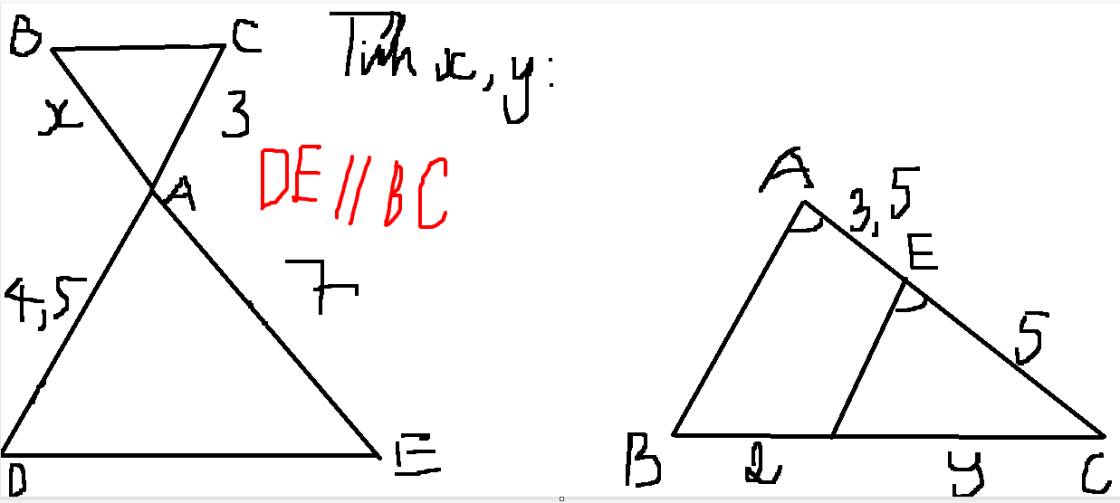Bổ sung hình bên phải:
Giả:
Gọi chân đường thẳng điểm E hạ xuống cạnh BC là F.
Ta có: \(\widehat{CEF}=\widehat{EAB}\)
Mà hai góc này ở vị trí đồng vị.
=> AB // EF
Áp dụng định lý talet vào tam giác ABC có:
\(\dfrac{CE}{EA}=\dfrac{CF}{FB}\\ \Leftrightarrow\dfrac{5}{3,5}=\dfrac{y}{2}\\ \Leftrightarrow y=\dfrac{5}{3,5}.2=\dfrac{20}{7}\)
Xét ΔABC và ΔAED có
góc ABC=góc AED
góc BAC=góc EAD
=>ΔABC đồng dạng vớiΔAED
=>AB/AE=AC/AD
=>x/7=3/4,5=2/3
=>x=14/3
a) Ta có: \(DE\text{//}BC\)
\(\Rightarrow\Delta ABC\sim\Delta AED\)
\(\Rightarrow\dfrac{AC}{AD}=\dfrac{AB}{AE}\) hay \(\dfrac{3}{4,5}=\dfrac{x}{7}\)
\(\Rightarrow x=\dfrac{3\cdot7}{4,5}=4,2\left(cm\right)\)
b) Ta có: \(\widehat{A}=\widehat{E}\) (đồng vị)
\(\Rightarrow\text{ED//}AB\)
\(\Rightarrow\Delta ABC\sim\Delta EDC\)
\(\Rightarrow\dfrac{EC}{AC}=\dfrac{DC}{BC}\) hay \(\dfrac{5}{8,5}=\dfrac{y}{2+y}\)
\(\Rightarrow5\left(2+y\right)=8,5y\)
\(\Leftrightarrow10+5y=8,5y\)
\(\Leftrightarrow10=3,5y\)
\(\Leftrightarrow y=\dfrac{10}{3,5}\approx2,85\left(cm\right)\)