2: a: 3x^2-11x+8=0
a=3; b=-11; c=8
a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
x1=1 và x2=c/a=8/3
b: x^2-(1+căn 3)x+căn 3=0
a+b+c=0
nên phương trình có hai nghiệm pb là:
x1=1 và x2=căn 3
c: 5x^2+24x+19=0
a-b+c=0 nên phương trình có hai nghiệm là:
x1=-1 và x2=-c/a=-19/5
d: x^2-12x+27=0
=>(x-3)(x-9)=0
=>x=3 hoặc x=9
e: x^2-10x+21=0
=>(x-3)(x-7)=0
=>x=3 hoặc x=7
f: (1-căn2)*x^2-2(1+căn 2)x+1+3căn 2=0
Vì a+b+c=0
nên phương trình có hai nghiệm là:
x1=1 và x2=c/a=(1+3căn 2)/(1-căn 2)=-7-4căn 2
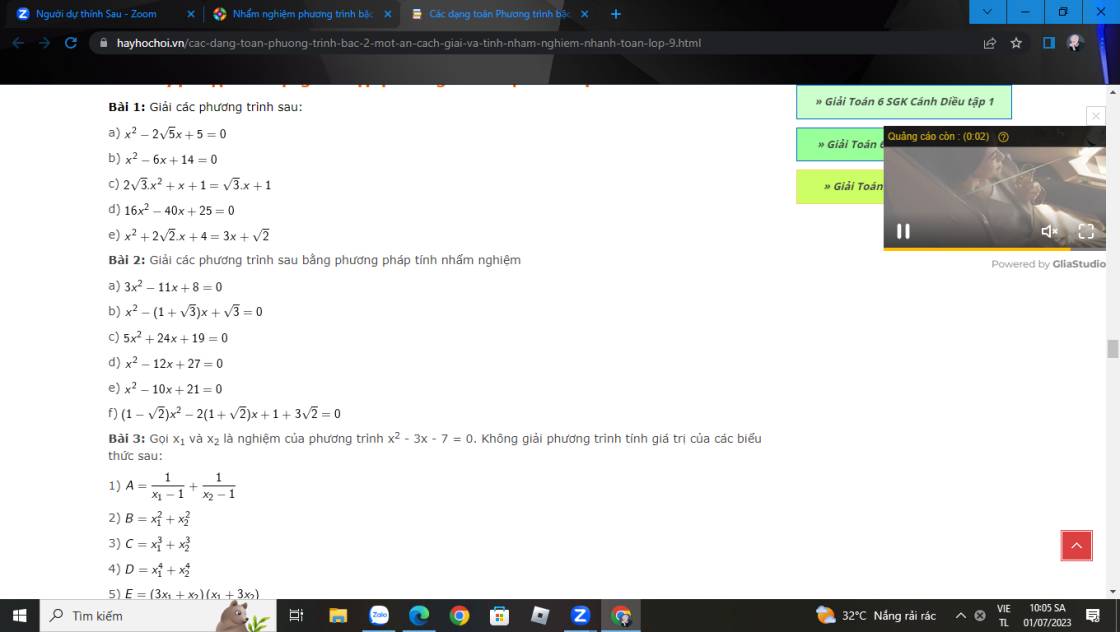
Bài 1:
a) \(x^2-2\sqrt{5}x+5=0\)
\(\Rightarrow\Delta=\left(-2\sqrt{5}\right)^2-4\cdot1\cdot5=0\)
Pt có nghiệm kép:
\(x_1=x_2=\dfrac{-\left(-2\sqrt{5}\right)}{2\cdot1}=\sqrt{5}\)
b) \(x^2-6x+14=0\)
\(\Rightarrow\Delta=\left(-6\right)^2-4\cdot1\cdot14=-20< 0\)
Pt vô nghiệm
c) \(2\sqrt{3}x^2+x+1=\sqrt{3}x+1\)
\(\Leftrightarrow2\sqrt{3}x^2+x+1-\sqrt{3}x-1=0\)
\(\Leftrightarrow2\sqrt{3}x^2+\left(1-\sqrt{3}\right)x=0\)
\(\Rightarrow\Delta=\left(1-\sqrt{3}\right)^2-4\cdot2\sqrt{3}\cdot0=4-2\sqrt{3}>0\)
Pt có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-\left(1-\sqrt{3}\right)+\sqrt{4-2\sqrt{3}}}{2\cdot1}\approx0,7\\x_2=\dfrac{-\left(1+\sqrt{3}\right)-\sqrt{4-2\sqrt{3}}}{2\cdot1}=0\end{matrix}\right.\)
d) \(16x^2-40x+25=0\)
\(\Leftrightarrow\left(4x\right)^2-2\cdot4x\cdot5+5^2=0\)
\(\Leftrightarrow\left(4x-5\right)^2=0\)
\(\Leftrightarrow4x-5=0\)
\(\Leftrightarrow4x=5\)
\(\Leftrightarrow x=\dfrac{5}{4}\)
e) \(x^2+2\sqrt{2}x+4=3x+\sqrt{2}\)
\(\Leftrightarrow x^2+2\sqrt{2}x+4-3x-\sqrt{2}=0\)
\(\Leftrightarrow x^2+\left(2\sqrt{2}-3\right)x+\left(4-\sqrt{2}\right)=0\)
\(\Rightarrow\Delta=\left(2\sqrt{2}-3\right)^2-4\cdot1\cdot\left(4-\sqrt{2}\right)=1-8\sqrt{2}< 0\)
Vậy Pt vô nghiệm