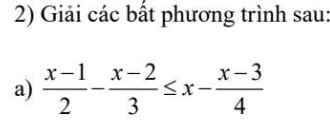\(\dfrac{x-1}{2}-\dfrac{x-2}{3}\le x-\dfrac{x-3}{4}\\ \Leftrightarrow\dfrac{\left(x-1\right)6}{2.6}-\dfrac{\left(x-2\right)4}{3.4}\le\dfrac{x.12}{1.12}-\dfrac{\left(x-3\right)3}{4.3}\\ \Leftrightarrow6x-6-4x+8\le12x-3x+9\\ \Leftrightarrow6x-4x-12x+3x\le9+6-8\\ \Leftrightarrow-7x\le7\\ \Leftrightarrow x\ge-1\)
Vậy bất phương trình có nghiệm là:\(S=\left\{x|x\ge-1\right\}\)
\(\dfrac{x-1}{2}-\dfrac{x-2}{3}\le x-\dfrac{x-3}{4}\)
\(\Leftrightarrow\dfrac{6\left(x-1\right)}{12}-\dfrac{4\left(x-2\right)}{12}\le\dfrac{12x}{12}-\dfrac{3\left(x-3\right)}{12}\)
\(\Leftrightarrow6x-6-4x+8\le12x-3x+9\)
\(\Leftrightarrow2x+2\le9x+9\)
\(\Leftrightarrow2x-9x\le-2+9\)
\(\Leftrightarrow-7x\le7\)
\(\Leftrightarrow x\ge-1\)
\(\text{Vậy bất phương trình có tập nghiệm là }\left\{x/x\ge-1\right\}\)
a: =>6(x-1)-4(x-2)<=12x-3(x-3)
=>6x-6-4x+8<=12x-3x+9
=>2x+2<=9x+9
=>-7x-7<=0
=>-7x<=7
=>x>=-1