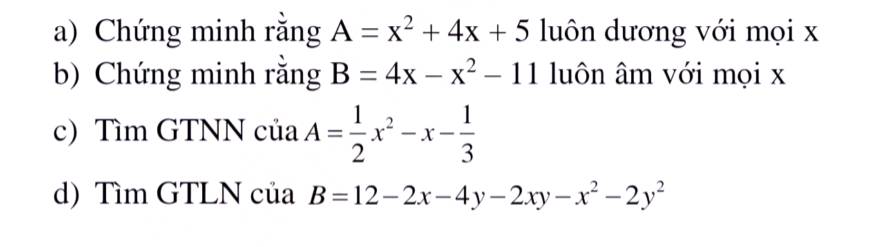\(a,A=\left(x^2+4x+4\right)+1\\ =\left(x+2\right)^2+1\ge1>0\forall x\)
=> A luôn dương với mọi x
\(b,B=-\left(x^2-4x+11\right)\\ =-\left(x^2-4x+4+7\right)\\ =-\left(x-2\right)^2-7\le-7< 0\forall x\\ \)
Vậy B luôn âm với mọi x
c: \(A=\dfrac{1}{2}\left(x^2-2x-\dfrac{2}{3}\right)\)
\(=\dfrac{1}{2}\left(x^2-2x+1-\dfrac{5}{3}\right)\)
\(=\dfrac{1}{2}\left(x-1\right)^2-\dfrac{5}{6}>=-\dfrac{5}{6}\)
Dấu '=' xảy ra khi x=1
d) \(B=12-2x-4y-2xy-x^2-2y^2\)
\(-B=2x+4y+2xy+x^2+2y^2-12\)
\(=\left(x^2+y^2+1+2xy+2x+2y\right)+\left(y^2+2y+1\right)-14\)
\(=\left[\left(x+y\right)^2+2\left(x+y\right)+1\right]+\left(y+1\right)^2-14\)
\(=\left(x+y+1\right)^2+\left(y+1\right)^2-14\ge-14\)
\(\Rightarrow B\le14\)
- Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\left(x+y+1\right)^2=0\\\left(y+1\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-1\end{matrix}\right.\)
- Vậy \(MinB=14\).