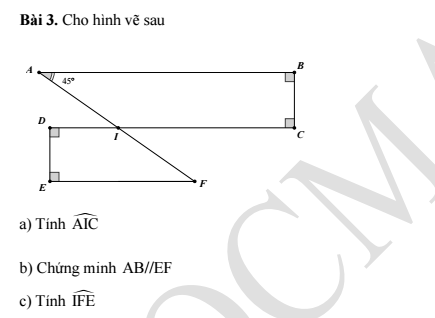
`hat(AIC) cùng phía `hat(IAB)` mà `AB //// IC`
`=> hat(AIC) = 180^o - 45^o = 135 ^o`
Ta có: `AB` vuông góc `BC, BC` vuông góc `CD`
`=> AB //// CD`
`ED` vuông góc với `DC, EF` vuông góc `DC`
`=> DC //// EF`
`=> AB //// EF`.
`=> hat(IFE) = hat( IAB) = 45^o (` So le trong `)`.
`a)` Vì `AB \bot BC` mà `IC \bot BC`
`=>AB //// IC=>\hat{A}+\hat{AIC}=180^o`
`=>45^o +\hat{AIC}=180^o =>\hat{AIC}=135^o`
`b)` Vì `DI \bot DE` mà `DE \bot EF`
`=>DI //// EF` Mà `DI /////AB`
`=>AB //// EF`
`c)` Vì `AB //// EF=>\hat{A}=\hat{F}` (`2` góc slt)
`=>\hat{F}=45^o` Hay `\hat{IFE}=45^o`
`a)`Xét tứ giác `ABCD` có:
\(\widehat{AIC}=360^o-45^o-90^o-90^o=135^o\)
`b)`Ta có:\(ED\perp CD\) ( gt )
\(BC\perp CD\) ( gt )
\(\Rightarrow ED\backslash\backslash BC\)
Mà \(AB\perp BC\)
\(EF\perp DE\)
\(\Rightarrow AB\backslash\backslash EF\)
`c)`Ta có: \(\widehat{BAI}=\widehat{IFE}=45^o\) ( so le trong vì \(AB\backslash\backslash EF\) )