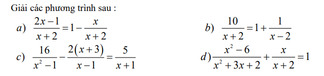a.\(ĐK:x\ne-2\)
\(\Leftrightarrow\dfrac{2x-1}{x+2}=\dfrac{\left(x+2\right)-x}{x-2}\)
\(\Leftrightarrow2x-1=2\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=\dfrac{3}{2}\left(tm\right)\)
b.\(ĐK:x\ne\pm2\)
\(\Leftrightarrow\dfrac{10}{x+2}=\dfrac{\left(x-2\right)+1}{x-2}\)
\(\Leftrightarrow10=x-1\)
\(\Leftrightarrow x=11\left(tm\right)\)
c.\(ĐK:x\ne\pm1\)
\(\Leftrightarrow\dfrac{16}{\left(x-1\right)\left(x+1\right)}=\dfrac{5}{x+1}+\dfrac{2\left(x-3\right)}{x-1}\)
\(\Leftrightarrow\dfrac{16}{\left(x-1\right)\left(x+1\right)}=\dfrac{5\left(x-1\right)+\left(2x+6\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Leftrightarrow16=5x-5+2x^2+2x+6x+6\)
\(\Leftrightarrow2x^2+13x-17=0\)
d.\(x\ne\pm2;x\ne-1\)
\(\Leftrightarrow\dfrac{x^2-6}{\left(x+1\right)\left(x+2\right)}=1-\dfrac{x}{x+2}\)
\(\Leftrightarrow\dfrac{x^2-6}{\left(x+1\right)\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)-x\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}\)
\(\Leftrightarrow x^2-6=x^2+2x+x+2-x^2-x\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=-2\left(ktm\right)\end{matrix}\right.\)
a, x khác -2
\(\dfrac{2x-1}{x+2}=\dfrac{x+2-x}{x+2}\Rightarrow2x-1=2\Leftrightarrow x=\dfrac{3}{2}\left(tm\right)\)
b, đk : x khác -2 ; 2
\(\Rightarrow10\left(x-2\right)=x^2-4+x+2\Leftrightarrow x^2+x-2-10x+20\Leftrightarrow x^2-9x+18=0\)
\(\Leftrightarrow\left(x-6\right)\left(x-3\right)=0\Leftrightarrow x=6\left(tm\right);x=3\left(tm\right)\)
c, đk : x khác 1 ; -1 \(\Rightarrow16-2\left(x^2+4x+3\right)=5x-5\Leftrightarrow-2x^2-8x+10=5x-5\)
\(\Leftrightarrow-2x^2-13x+15=0\Leftrightarrow x=1\left(ktm\right);x=-\dfrac{15}{2}\)
d,
đk : x khác -2 ; -1 \(\Rightarrow x^2-6+x\left(x+1\right)=x^2+3x+2\Leftrightarrow2x^2+x-6=x^2+3x+2\)
\(\Leftrightarrow x^2-2x-8=0\Leftrightarrow\left(x-1\right)^2-9=0\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\Leftrightarrow x=4;x=-2\left(ktm\right)\)
a: \(\Leftrightarrow2x-1=x+2-x\)
=>2x-1=2
hay x=3/2(nhận)
b: \(\Leftrightarrow10\left(x-2\right)=x^2-4+x+2\)
\(\Leftrightarrow x^2+x-2-10x+20=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>(x-3)(x-6)=0
=>x=3(nhận) hoặc x=6(nhận)
c: \(\Leftrightarrow16-2\left(x+3\right)\left(x+1\right)=5\left(x-1\right)\)
\(\Leftrightarrow16-2\left(x^2+4x+4\right)-5x+5=0\)
\(\Leftrightarrow-2x^2-8x-8-5x+11=0\)
\(\Leftrightarrow-2x^2-13x+3=0\)
\(\Leftrightarrow2x^2+13x-3=0\)
\(\text{Δ}=13^2-4\cdot2\cdot\left(-3\right)=169+24=193>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{13-\sqrt{193}}{4}\\x_2=\dfrac{13+\sqrt{193}}{4}\end{matrix}\right.\)
d: \(\Leftrightarrow x^2-6+x\left(x+1\right)=x^2+3x+2\)
\(\Rightarrow x^2+x-6-3x-2=0\)
\(\Leftrightarrow x^2-2x-8=0\)
=>(x-4)(x+2)=0
=>x=4(nhận) hoặc x=-2(loại)
Thấy tội k ai giúp :))
\(a,\Leftrightarrow\dfrac{2x-1}{x+2}=1-\dfrac{x}{x+2}\\ \Leftrightarrow\left\{{}\begin{matrix}2x-1=\left(x+2\right)\left(1-\dfrac{x}{x+2}\right)\\x+2\ne0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\x+2\ne0\end{matrix}\right.\Rightarrow x=\dfrac{3}{2}\)
\(b,\\ \Leftrightarrow\dfrac{10}{x+2}=\dfrac{x-2+1}{x-2}\Leftrightarrow\dfrac{10}{x+2}=\dfrac{x-1}{x-2}\\ \Leftrightarrow10\left(x-2\right)=\left(x+2\right)\left(x-1\right)\\ \Leftrightarrow10x-20=x^2+x-2\\ \Leftrightarrow x^2-9x+18=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=3\end{matrix}\right.\)
\(c,\\ \Leftrightarrow\dfrac{5}{x+1}=\dfrac{16}{x^2-1}-\dfrac{2\left(x+3\right)}{x-1}\\ \Leftrightarrow\left\{{}\begin{matrix}5=-2x-10\\x+1\ne0\end{matrix}\right.\Rightarrow x=-\dfrac{15}{2}\\ d,\\ \Leftrightarrow\dfrac{2x-3}{x+1}=1\Leftrightarrow\left\{{}\begin{matrix}2x-3=\left(x+1\right).1\\x+1\ne0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=4\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\5\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\có.vô.số.n_o\end{matrix}\right.\)
a, \(\dfrac{2x-1}{x+2}-1+\dfrac{x}{x+2}=0\)
\(\dfrac{2x-1}{x+2}-\dfrac{x+2}{x+2}+\dfrac{x}{x+2}=0\)
\(\dfrac{2x-3}{x+2}=0\)
2x-3=0
x=\(\dfrac{3}{2}\)
b, \(\dfrac{10}{x+2}-1-\dfrac{1}{x-2}=0\)
\(\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=0\)
\(\dfrac{-x^2+9x-18}{\left(x-2\right)\left(x+2\right)}=0\)
\(\dfrac{\left(x-3\right)\left(x-6\right)}{\left(x-2\right)\left(x+2\right)}=0\)
(x-3)(x-6)=0
<=>x=3 hoặc x=6