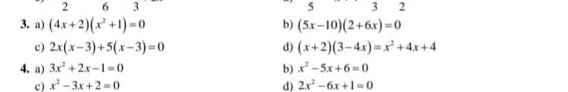\(3,\\ a,\left(4x+2\right).\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x+2=0\\x^2+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}4x=2\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\\ \Leftrightarrow x=\dfrac{1}{2}\\ \Rightarrow S=\left\{\dfrac{1}{2}\right\}\\ b,\left(5x-10\right).\left(2+6x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-10=0\\2+6x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}5x=10\\6x=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{1}{3}\end{matrix}\right.\\ \Rightarrow S=\left\{-\dfrac{1}{3};2\right\}\)
\(c,2x.\left(x-3\right)+5\left(x-3\right)=0\\ \Leftrightarrow\left(2x+5\right).\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+5=0\\x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=3\end{matrix}\right.\\ \Rightarrow S=\left\{-\dfrac{5}{2};3\right\}\\ d,\left(x+2\right).\left(3-4x\right)=x^2+4x+4\\ \Leftrightarrow\left(x+2\right).\left(3-4x\right)=\left(x+2\right)^2\\ \Leftrightarrow\left(x+2\right).\left(3x-4\right)-\left(x+2\right)^2=0\\ \Leftrightarrow\left(x+2\right).\left(3x-4-x-2\right)=0\\ \Leftrightarrow\left(x+2\right).\left(2x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\\ \Rightarrow S=\left\{-2;3\right\}\)