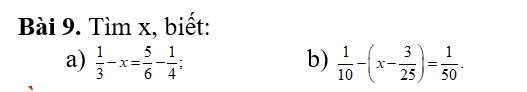Question

Answer 1

     \(\dfrac{1}{3}-x=\dfrac{5}{6}-\dfrac{1}{4}\)

⇔ \(\dfrac{1}{3}-x=\dfrac{7}{12}\)

⇔         \(x=\dfrac{-1}{4}\)

Answer 2

a: \(\dfrac{1}{3}-x=\dfrac{5}{6}-\dfrac{1}{4}\)

\(\Leftrightarrow\dfrac{1}{3}-x=\dfrac{7}{12}\)

\(\Leftrightarrow x=\dfrac{1}{3}-\dfrac{7}{12}=\dfrac{4-7}{12}=\dfrac{-1}{4}\)

b: \(\dfrac{1}{10}-\left(x-\dfrac{3}{25}\right)=\dfrac{1}{50}\)

\(\Leftrightarrow x-\dfrac{3}{25}=\dfrac{2}{25}\)

hay \(x=\dfrac{1}{5}\)

Answer 3

a. \(\dfrac{1}{3}-x=\dfrac{5}{6}-\dfrac{1}{4}\)

<=> \(-x=\dfrac{5}{6}-\dfrac{1}{4}-\dfrac{1}{3}\)

<=> \(-x=\dfrac{1}{4}\)

<=> \(x=\dfrac{-1}{4}\)

b. \(\dfrac{1}{10}-\left(x-\dfrac{3}{25}\right)=\dfrac{1}{50}\)

<=> \(\dfrac{1}{10}-x+\dfrac{3}{25}=\dfrac{1}{50}\)

<=> \(-x=\dfrac{1}{50}-\dfrac{1}{10}-\dfrac{3}{25}\)

<=> \(-x=\dfrac{-1}{5}\)

<=> \(x=\dfrac{1}{5}\)

Answer 4

   \(\dfrac{1}{10}-\left(x-\dfrac{3}{25}\right)=\dfrac{1}{50}\)

⇔              \(x-\dfrac{3}{25}=\dfrac{2}{25}\)

⇔                       \(x=\dfrac{1}{5}\)

Answer 5

\(a\)) \(\dfrac{1}{3}-x=\dfrac{5}{6}-\dfrac{1}{4}\)                                          \(b\)) \(\dfrac{1}{10}-\left(x-\dfrac{3}{25}\right)=\dfrac{1}{50}\)

     \(\dfrac{1}{3}-x=\dfrac{7}{12}\)                                                    \(x-\dfrac{3}{25}=\dfrac{1}{50}+\dfrac{1}{10}\)

      \(x=\dfrac{1}{3}-\dfrac{7}{12}\)                                                   \(x-\dfrac{3}{25}=\dfrac{3}{25}\)

      \(x=-\dfrac{1}{4}\)                                                          \(x=\dfrac{3}{25}+\dfrac{3}{25}\)

                                                                              \(x=\dfrac{6}{25}\)