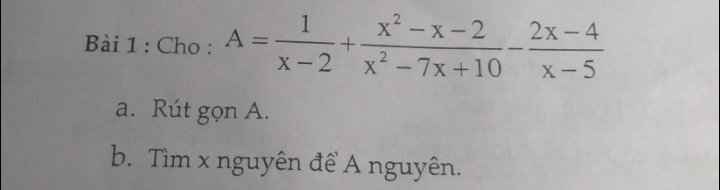a, \(A=\dfrac{1}{x-2}+\dfrac{x^2-x-2}{x^2-7x+10}-\dfrac{2x-4}{x-5}\)ĐK : \(x\ne2;5\)
\(=\dfrac{x-5+x^2-x-2-\left(2x-4\right)\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}\)
\(=\dfrac{x-5+x^2-x-2-2\left(x-2\right)^2}{\left(x-2\right)\left(x-5\right)}=\dfrac{x^2-7-2\left(x^2-4x+4\right)}{\left(x-2\right)\left(x-5\right)}\)
\(=\dfrac{x^2-7-2x^2+8x-8}{\left(x-2\right)\left(x-5\right)}=\dfrac{-x^2-15+8x}{\left(x-2\right)\left(x-5\right)}=\dfrac{3-x}{x-2}\)
b, Ta có : \(\dfrac{3-x}{x-2}=-\dfrac{x-3}{x-2}=-\dfrac{x-2-1}{x-2}=-1-\dfrac{1}{x-2}\)
Vì -1 nguyên nên \(-\dfrac{1}{x-2}\)cũng phải nguyên
\(x-2\inƯ\left(-1\right)=\left\{\pm1\right\}\)
| x - 2 | 1 | -1 |
| x | 3 | 1 |
Lời giải:
ĐKXĐ: $x\neq 2;5$
\(A=\frac{x-5}{(x-5)(x-2)}+\frac{x^2-x-2}{(x-2)(x-5)}-\frac{(2x-4)(x-2)}{(x-2)(x-5)}\)
\(=\frac{x-5+x^2-x-2-(2x^2-8x+8)}{(x-2)(x-5)}=\frac{-(x^2-8x+15)}{(x-2)(x-5)}=\frac{-(x-3)(x-5)}{(x-2)(x-5)}=\frac{3-x}{x-2}\)
b. Để $A$ nguyên thì $3-x\vdots x-2$
$\Leftrightarrow -(x-2)+1\vdots x-2$
$\Leftrightarrow 1\vdots x-2$
$\Rightarrow x-2\in\left\{\pm 1\right\}$
$\Leftrightarrow x\in\left\{3;1\right\}$ (đều tm)
a, \(A=\dfrac{1}{x-2}+\dfrac{x^2-x-2}{x^2-7x+10}-\dfrac{2x-4}{x-5}\)
\(A=\dfrac{1}{x-2}+\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}-\dfrac{2\left(x-2\right)}{x-5}\)
\(A=\dfrac{1}{x-2}+\dfrac{x+1}{x-5}-\dfrac{2\left(x-2\right)}{x-5}\)
\(A=\dfrac{1}{x-2}-\dfrac{x-5}{x-5}\)
\(A=\dfrac{1-x+2}{x-2}\)
b, \(A=\dfrac{1-x+2}{x-2}=\dfrac{1-\left(x-2\right)}{x-2}=\dfrac{1}{x-2}-1\)
Để A nguyên thì \(\dfrac{1}{x-2}\) nguyên
\(\Leftrightarrow x-2\in\left\{\pm1\right\}\)
\(\Leftrightarrow x\in\left\{1;3\right\}\)
Vậy \(x\in\left\{1;3\right\}\)
a) \(\dfrac{3-x}{x-2}\)
b) x thuộc Z
=> x=1
a) Ta có: \(A=\dfrac{1}{x-2}+\dfrac{x^2-x-2}{x^2-7x+10}-\dfrac{2x-4}{x-5}\)
\(=\dfrac{x-5+x^2-x-2-\left(2x-4\right)\left(x-2\right)}{\left(x-5\right)\left(x-2\right)}\)
\(=\dfrac{x^2-7-\left(2x^2-4x-4x+8\right)}{\left(x-5\right)\left(x-2\right)}\)
\(=\dfrac{x^2-7-2x^2+8x-8}{\left(x-5\right)\left(x-2\right)}\)
\(=\dfrac{-x^2+8x-15}{\left(x-5\right)\left(x-2\right)}\)
\(=\dfrac{-\left(x-5\right)\left(x-3\right)}{\left(x-5\right)\left(x-2\right)}\)
\(=\dfrac{-x+3}{x-2}\)
b) Để A nguyên thì \(-x+3⋮x-2\)
\(\Leftrightarrow1⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)