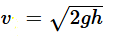
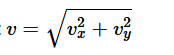
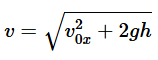
cho em hỏi ba công thức này thì khác gì nhau, áp dụng trong trường hợp nào với ạ
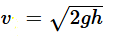
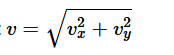
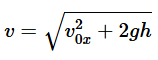
cho em hỏi ba công thức này thì khác gì nhau, áp dụng trong trường hợp nào với ạ
\(v=\sqrt{2gh}:\) Công thức này chỉ áp dụng cho trường hợp vật rơi tự do từ trạng thái nghỉ, không có vận tốc ban đầu theo phương ngang
\(v=\sqrt{v_x^2+v_y^2}:\) Công thức này áp dụng cho mọi trường hợp chuyển động có sự kết hợp của hai thành phần vận tốc vuông góc
\(v=\sqrt{v_{ox}^2+2gh}:\) Công thức này là sự kết hợp của hai công thức trên, dùng để tính vận tốc cuối cùng của một vật được ném ngang từ độ cao \(h\)
Một lực F = 100 N được phân tích theo hai phương Ox (Fx), Oy (Fy) như hình vẽ. Tìm hai thành phần Fx, Fy.
Cho một lực F = 100 N. Phân tích lực \(\overrightarrow{F}\) theo hướng Ox, Oy như hình vẽ (cho 2 trục Ox, Oy vuông góc với nhau tại O, \(\overrightarrow{F}\) xuất phát từ O tạo với Ox một góc 60°). Tính hai thành phần lực (Fx, Fy)
Cho hợp lực của hai lực F1 = 100 N, F2 = 100 N. Tính F trong các trường hợp sau:
a, \(\overrightarrow{F_{1}}\) cùng chiều với \(\overrightarrow{F_{2}}\)
b, \(\overrightarrow{F_{1}}\) ngược chiều với \(\overrightarrow{F_{2}}\)
c, \(\overrightarrow{F_{1}}\) \(\bot \) \(\overrightarrow{F_{2}}\)
d, \(\overrightarrow{F_{1}} \cdot \overrightarrow{F_{2}} = 180^\circ \)
Ta có: \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
a, \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow F=F_1+F_2=100+100=200N\)
b, \(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow F=\left|F_1-F_2\right|=\left|100-100\right|=0N\)
c, \(\overrightarrow{F_1}\perp\overrightarrow{F_2}\Rightarrow F=\sqrt{F_1^2+F_2^2}=\sqrt{100^2+100^2}=\sqrt{20000}N\)
d, \(\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)=180^o\Rightarrow F=\sqrt{F_1^2+F_2^2+2.F_1.F_2.cos180^o}\)
\(\Rightarrow F=\sqrt{100^2+100^2+2.100.100.cos180^o}\)
\(\Rightarrow F=0N\)
Phân tích lực F = 100 N theo hướng Ox, Oy như hình vẽ (cho 2 trục Ox, Oy vuông góc với nhau tại O, \(\overrightarrow{F}\) xuất phát từ O tạo với Ox một góc 30°). Tính hai thành phần lực đã phân tích
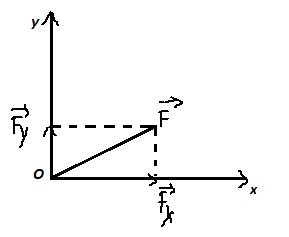
\(\overrightarrow{F_x}\perp\overrightarrow{F_y}\) \(\Rightarrow cos30^o=\dfrac{F_x}{F}\)\(\Rightarrow F_x=F.cos30^o=100.cos30^o=50\sqrt{3}\left(N\right)\)
Ta co': \(F_y=\sqrt{F^2-F_y^2}=\sqrt{100^2-\left(50\sqrt{3}\right)^2}=50\left(N\right)\) (theo đinh lý pytago)
Vậy \(F_x=50\sqrt{3}N,F_y=50N\)
Trên một dốc nghiêng α=30°, buông một vật nhỏ từ A. Vật nhỏ trượt xuống dốc nhẵn. Sau khi buông vật này 1 giây, cũng từ A bắn một viên bi nhỏ theo phương ngang với vận tốc đầu v. Xác định v để bi trúng vào vật trượt trên dốc nghiêng. Bỏ qua lực cản của không khí. Lấy g=10m/s^2
Tìm phát biểu đúng sau đây:
A. Không có lực tác dụng, vật không chuyển động
B. Ngừng tác dụng lực, vật sẽ dừng lại
C. Gia tốc của vật nhất thiết theo hướng của lực
D. Khi tác dụng lực lên vật, vận tốc của vật tăng
C. Gia tốc của vật nhất thiết theo hướng của lực. Theo định luật thứ hai của Newton, gia tốc của vật luôn theo hướng của lực tác dụng lên nó.
Một hòn đá có trọng lượng 10N đc thả từ độ cao 4m so vs đất rồi nó đào sau vào đất thêm 1 đoạn 20cm. Coi chuyển động của hòn đá trong ko khí và trong đất là cđ biến đổi đều, biết lực cản không khí là 2N. Hãy tìm lực cản trong đất.
Gọi \(\overrightarrow{F_c};\overrightarrow{F_c'}\) là lực cản của không khí và lực cản của đất lên hòn đá
\(m\left(kg\right):\) là khối lượng của hòn đá
Giai đoạn \(1\): Rơi tự do trong không khí
\(\overrightarrow{P}+\overrightarrow{F_c}=m\overrightarrow{a_1}\)
\(\Rightarrow P-F_c=ma_1\)
\(\Rightarrow a_1=\dfrac{P-F_c}{m}=\dfrac{10-2}{m}=\dfrac{8}{m}\left(m/s^2\right)\)
Giai đoạn \(2\): Đâm vào đất
\(\overrightarrow{P}+\overrightarrow{F_c'}=m\overrightarrow{a_2}\)
\(\Rightarrow F_c'-P=ma_2\)
\(\Rightarrow a_2=\dfrac{F_c'-10}{m}\left(m/s^2\right)\)
Áp dụng định lý động năng khi hòn đá chạm đất và khi đâm vào đất
\(\dfrac{1}{2}mv^2=\dfrac{8}{m}.h\) \(\left(h=4m\right)\)
\(\dfrac{1}{2}mv^2=\dfrac{F_c'-10}{m}.s\) \(\left(s=20cm=0,2m\right)\)
\(\Rightarrow\dfrac{8}{m}.h=\dfrac{F_c'-10}{m}.s\)
\(\Rightarrow F_c'=\dfrac{8h}{s}+10=\dfrac{8.4}{0,2}+10=170\left(N\right)\)
Vậy lực cản của đất tác dụng lên hòn đá là \(170\left(N\right)\)
Một ô tô khởi hành lúc 7 giờ. Nếu chọn mốc thời gian là 5 giờ thì thời điểm ban đầu là ?
Khoảng thời gian giữa 5 giờ và 7 giờ là 2 giờ. Vì vậy, khi chọn mốc thời gian là 5 giờ, thời điểm ban đầu (khi ô tô khởi hành) sẽ là 7 giờ, tức là 2 giờ sau mốc thời gian 5 giờ.