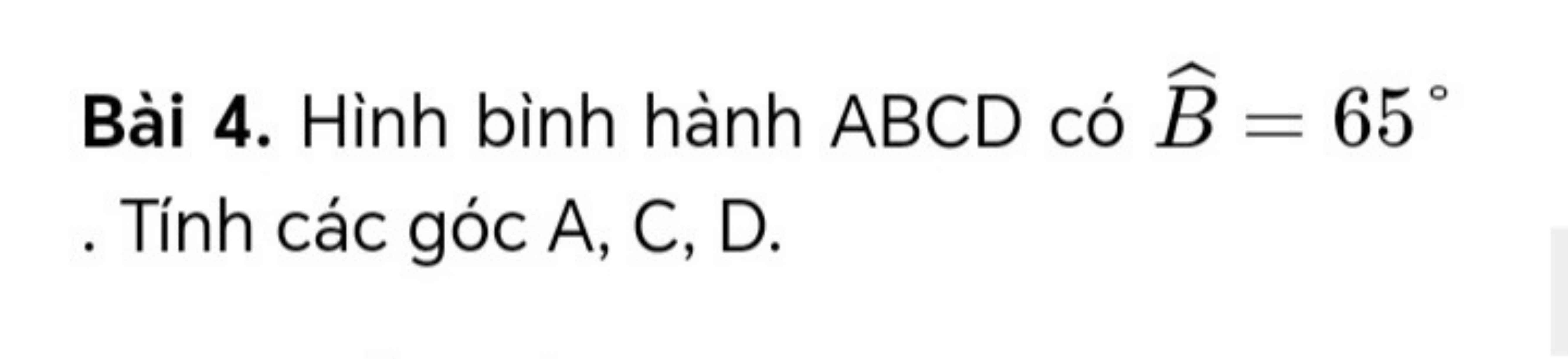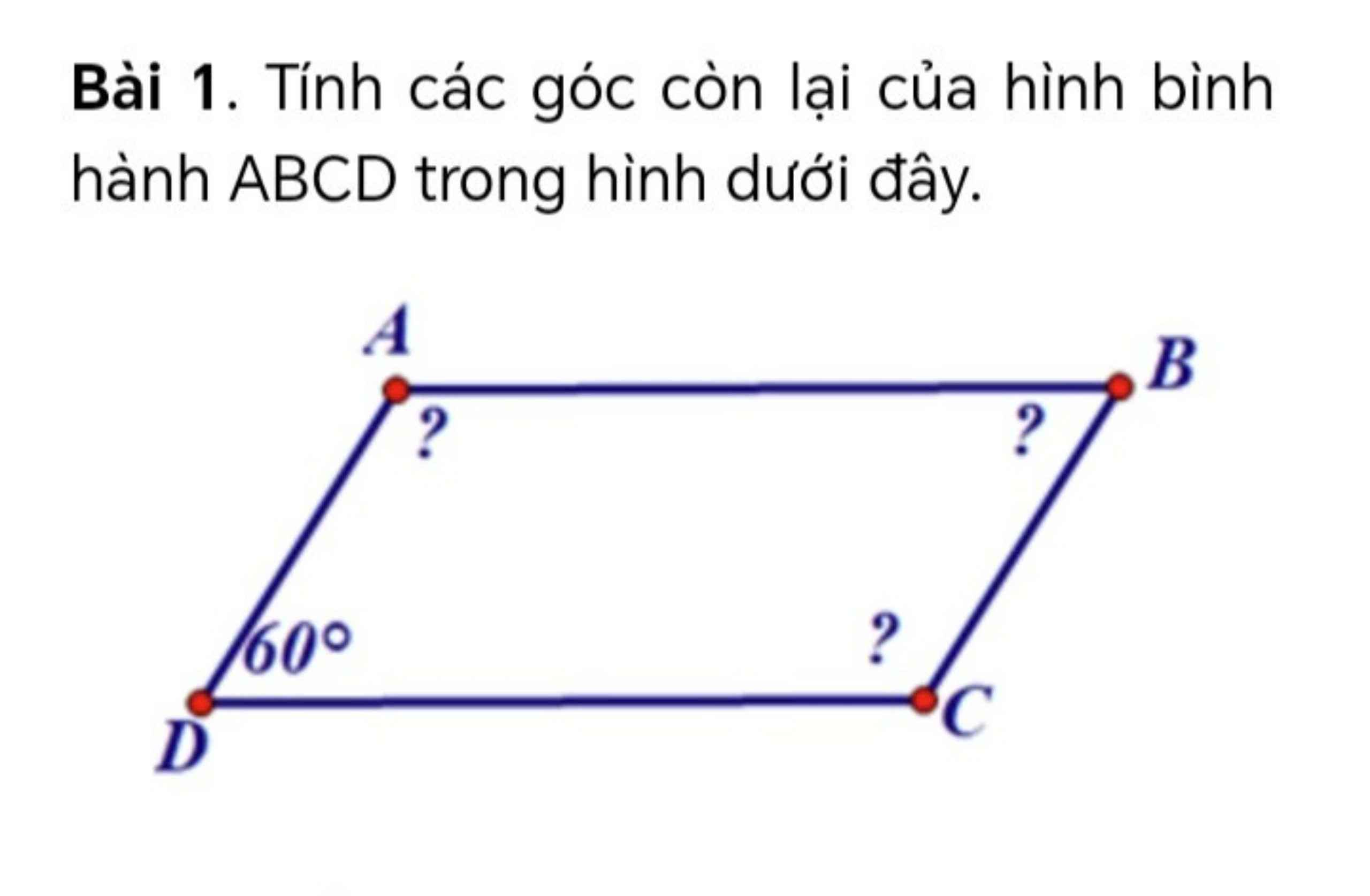
Ta có:D=B(theo định lí hình bình hành)

Do đó:B=60 độ

Mà A=C

Nên A=C=360-60+60

                 _________=120 độ

                        3

Vậy D=B=60 độ

A=C=120 độ

Tứ giác ABCD là hình bình hành.

\(\Rightarrow\)góc B=góc D(=65^o)(tính chất hình bình hành)

Lại có:góc B+góc A =180^o(2 góc trong cùng phía bù nhau)

\(\Rightarrow\)góc A =180^o-góc B=180^o-65^o=115^o

góc A = góc C (115^o)(tính chất hình bình hành)

a: Sửa đề: \(\dfrac{1}{x+2}+\dfrac{3}{x^2-4}+\dfrac{x-14}{\left(x^2+4x+4\right)\left(x-2\right)}\)

\(=\dfrac{1}{x+2}+\dfrac{3}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-14}{\left(x+2\right)^2\cdot\left(x-2\right)}\)

\(=\dfrac{x^2-4+3\left(x+2\right)+x-14}{\left(x+2\right)^2\cdot\left(x-2\right)}\)

\(=\dfrac{x^2+x-18+3x+6}{\left(x+2\right)^2\cdot\left(x-2\right)}\)

\(=\dfrac{x^2+4x-12}{\left(x+2\right)^2\cdot\left(x-2\right)}=\dfrac{\left(x+6\right)\left(x-2\right)}{\left(x+2\right)^2\cdot\left(x-2\right)}\)

\(=\dfrac{x+6}{\left(x+2\right)^2}\)

b: \(\dfrac{18}{\left(x-3\right)\left(x^2-9\right)}-\dfrac{3}{x^2-6x+9}-\dfrac{x}{x^2-9}\)

\(=\dfrac{18}{\left(x-3\right)^2\cdot\left(x+3\right)}-\dfrac{3}{\left(x-3\right)^2}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{18-3\left(x+3\right)+x\left(x-3\right)}{\left(x-3\right)^2\cdot\left(x+3\right)}\)

\(=\dfrac{18-3x-9+x^2-3x}{\left(x-3\right)^2\cdot\left(x+3\right)}\)

\(=\dfrac{x^2-6x+9}{\left(x-3\right)^2\cdot\left(x+3\right)}=\dfrac{1}{x+3}\)

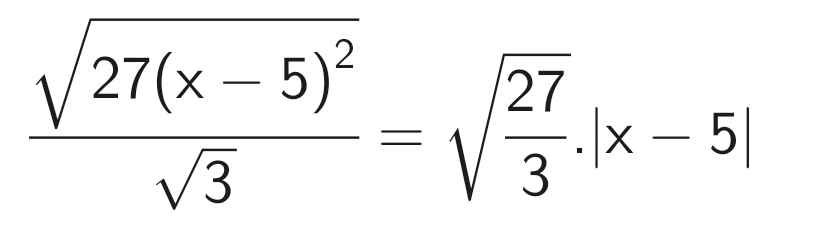
= 3|x - 5|   (1)

*) Với x ≥ 5, ta có:

(1) = 3(x - 5)

*) Với x < 5, ta có:

(1) = 3(5 - x)

\(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)

\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)

\(=\dfrac{11x+x-18}{2x-3}\)

\(=\dfrac{12x-18}{2x-3}=\dfrac{6\left(2x-3\right)}{2x-3}\)

=6

Xét tứ giác AEDF có \(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)

nên AEDF là hình chữ nhật

=>AF=DE; AE=DF

Xét ΔABC vuông tại A có AH là đường cao

nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2};AH\cdot BC=AB\cdot AC\)

Xét ΔADB vuông tại D có DE là đường cao

nên \(AE\cdot AB=AD^2\)(1)

Xét ΔADC vuông tại D có DF là đường cao

nên \(AF\cdot AC=AD^2\left(2\right)\)

Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)

Xét ΔABC có DE//AC

nên \(\dfrac{AE}{AB}=\dfrac{CD}{CB}\)

Xét ΔABC có DF//AB

nên \(\dfrac{AF}{AC}=\dfrac{BD}{BC}\)

\(\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{BD}{CB}+\dfrac{CD}{CB}=\dfrac{BD+DC}{BC}=\dfrac{BC}{BC}=1\)

=>\(\dfrac{AE}{AB}+\dfrac{AF}{AC}\) không đổi

a) a² − 4b² 

= a² − (2b)²
= (a −2b)(a + 2b)

b) 81(x+ 7)² - (3x + 8)²

= [9(x + 7)]² - (3x + 8)²

= (9x + 63)² - (3x + 8)²

= (9x + 63 - 3x - 8)(9x + 63 +3x + 8)
= (6x + 55)(12x + 71)

c) 4 - 4x + x² - 4y² - 4y - 1

= (x² - 4x + 4) - (4y² + 4y + 1)

= (x - 2)² - (2y + 1)²

= (x - 2 - 2y - 1)(x - 2 + 2y + 1)

= (x - 2y - 3)(x + 2y - 1)

\(x^2+\dfrac{1}{x^2}=7\\ \\ \\ \\ \Rightarrow x^2+2x\cdot\dfrac{1}{x}+\dfrac{1}{x^2}=7+2x\cdot\dfrac{1}{x}=9\\ \\ \\ \\ \Rightarrow\left(x+\dfrac{1}{x}\right)^2=9\\ \\ \\ \\ \Rightarrow x+\dfrac{1}{x}=\pm3\)

Trường hợp 1: \(x+\dfrac{1}{x}=3\) ta có:

\(x^3+\dfrac{1}{x^3}=\left(x^2+\dfrac{1}{x^2}\right)\left(x+\dfrac{1}{x}\right)-\left(x+\dfrac{1}{x}\right)=7\cdot3-3=18\)

Trường hợp 2: \(x+\dfrac{1}{x}=-3\) ta có:

\(x^3+\dfrac{1}{x^3}=\left(x^2+\dfrac{1}{x^2}\right)\left(x+\dfrac{1}{x}\right)-\left(x+\dfrac{1}{x}\right)=7\cdot\left(-3\right)-\left(-3\right)=-18\)

\(\dfrac{2x}{x^2-2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)

\(=\dfrac{2x}{x\left(x-2y\right)}+\dfrac{y}{y\left(x-2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)

\(=\dfrac{2}{x-2y}+\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)

\(=\dfrac{3}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}=\dfrac{3x+6y+4}{\left(x-2y\right)\left(x+2y\right)}\)