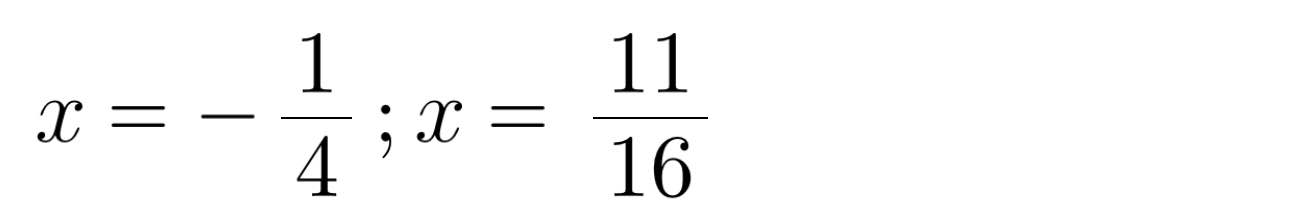Phân tích đa thức thành nhân tử :
a, a\(^2\) - 4b\(^2\)
b, 81( x + 7 )\(^2\) - ( 3x + 8 )\(^2\)
c, 4 - 4x + x\(^2\) - 4y\(^2\) - 4y - 1
d, y\(^2\) - 4xy + 4x\(^2\) - 16
e, 9x\(^2\) - 6x + 1 - (3x)\(^2\)
f, x\(^3\) + 3x\(^2\)y + 3xy\(^2\) + y\(^3\) + x + y
Tìm x, biết :
a, x\(^3\) + 27 + ( x + 3 ).( x - 9 ) = 0
b, x\(^4\) - 6x\(^3\) + 12x\(^2\) - 8x = 0
c, 36( x - 1 )\(^2\) - 25( 2x - 1 )\(^2\) = 0
b) 81(x+ 7)² - (3x + 8)²
= [9(x + 7)]² - (3x + 8)²
= (9x + 63)² - (3x + 8)²
= (9x + 63 - 3x - 8)(9x + 63 +3x + 8)
= (6x + 55)(12x + 71)
c) 4 - 4x + x² - 4y² - 4y - 1
= (x² - 4x + 4) - (4y² + 4y + 1)
= (x - 2)² - (2y + 1)²
= (x - 2 - 2y - 1)(x - 2 + 2y + 1)
= (x - 2y - 3)(x + 2y - 1)
d) y² - 4xy + 4x² - 16
= (y² - 4xy + 4x²) - 16
= (y - 2x)² - 4²
= (y - 2x - 4)(y - 2x + 4)
e) 9x² - 6x + 1 - (3x)²
= (9x² - 6x + 1) - (3x)²
= (3x - 1)² - (3x)²
= (3x - 1 - 3x)(3x - 1 + 3x)
= -(6x - 1)
= 1 - 6x
f) x³ + 3x²y + 3xy² + y³ + x + y
= (x³ + 3x²y + 3xy² + y³) + (x + y)
= (x + y)³ + (x + y)
= (x + y)[(x + y)² + 1]
= (x + y)(x² + 2xy + y² + 1)
Tìm x
a) x³ + 27 + (x + 3)(x - 9) = 0
(x³ + 27) + (x + 3)(x - 9) = 0
(x + 3)(x² - 3x + 9) + (x + 3)(x - 9) = 0
(x + 3)(x² - 3x + 9 + x - 9) = 0
(x + 3)(x² - x) = 0
x(x + 3)(x - 2) = 0
x = 0 hoặc x + 3 = 0 hoặc x - 2 = 0
*) x + 3 = 0
x = -3
*) x - 2 = 0
x = 2
Vậy x = -3; x = 0; x = 2
Tìm x
b) x⁴ - 6x³ + 12x² - 8x = 0
x(x³ - 6x² + 12x - 8) = 0
x(x - 2)³ = 0
x = 0 hoặc (x - 2)³ = 0
*) (x - 2)³ = 0
x - 2 = 0
x = 2
Vậy x = 0; x = 2
Tìm x
c) 36(x - 1)² - 25(2x - 1)² = 0
[6(x - 1)]² - [5(2x - 1)]² = 0
(6x - 6)² - (10x - 5)² = 0
(6x - 6 - 10x + 5)(6x - 6 + 10x - 5) = 0
(-4x - 1)(16x - 11) = 0
-4x - 1 = 0 hoặc 16x - 11 = 0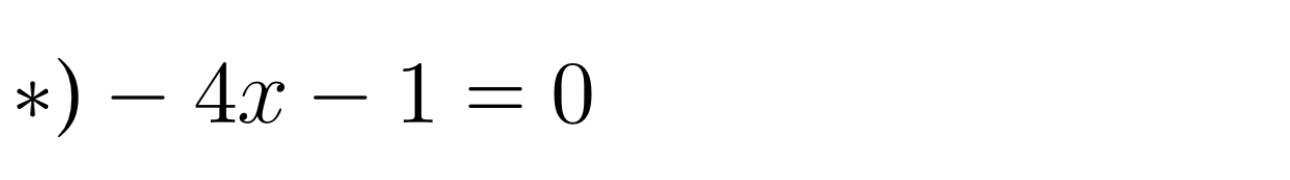


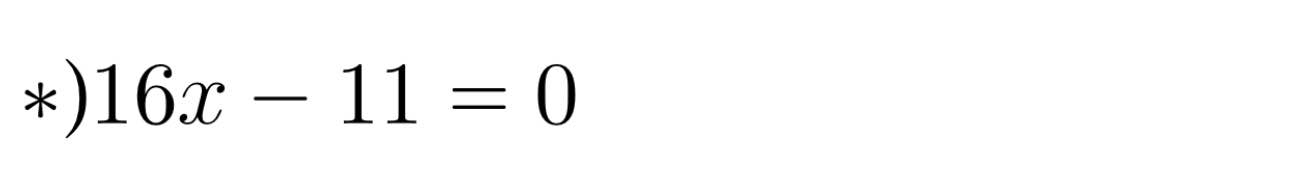


Vậy: