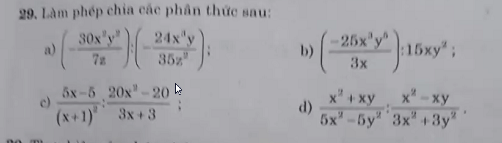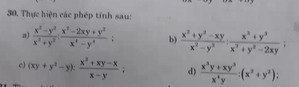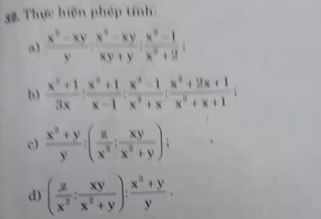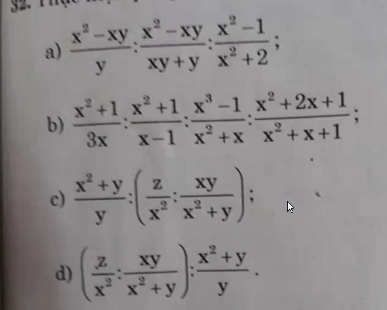Bài 8: Phép chia các phân thức đại số

VD1:

\(a,=\dfrac{\left(1-x\right)\left(1+x\right)}{x\left(x-2\right)}\cdot\dfrac{x}{x+1}=\dfrac{1-x}{x-2}\\ b,=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x+2}\cdot\dfrac{1}{x^2+x+1}=\dfrac{x-1}{x+2}\\ c,=\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+2\right)\left(x-1\right)}\cdot\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-1\right)^2}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)^2}\\ d,=\dfrac{x+2y}{x^2+xy+y^2}\cdot\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x+2y\right)^2}=\dfrac{x-y}{x+2y}\)

VD2:

\(a,A=\dfrac{x^2}{\left(y+1\right)^2}\cdot\dfrac{y+1}{2x}\cdot\dfrac{y+1}{2x}=\dfrac{1}{4}\\ b,B=\dfrac{x^2}{\left(y+1\right)^2}:\left(\dfrac{2y}{y+1}\cdot\dfrac{y+1}{2x}\right)=\dfrac{x^2}{\left(y+1\right)^2}\cdot1=\dfrac{x^2}{\left(y+1\right)^2}\)

VD1:

\(a,\dfrac{6x}{15y^3}\left(-\dfrac{5y^2}{3x^2}\right)=\dfrac{-2}{3xy}\\ b,=\dfrac{x+1}{x-2}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x+1\right)^2}=\dfrac{x+2}{x+1}\\ c,=\dfrac{-3\left(x-1\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x-1}=\dfrac{-3}{x+3}\\ d,=\dfrac{2\left(3x+2\right)}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-2\right)}{3x+2}=\dfrac{2x}{x+2}\)

a: \(A=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)

\(=\dfrac{6\left(x+1\right)\cdot x}{3\left(x+1\right)\left(x-2\right)}=\dfrac{2x}{x-2}\)

\(\dfrac{A}{B}=\dfrac{2x^2-x+4x-2}{2x-1}=x+2\)

a: \(=\dfrac{30x^2y^2}{7z}\cdot\dfrac{35z^3}{24x^2y}=\dfrac{5}{4}y\cdot5z^2=\dfrac{25yz^2}{4}\)

b: \(=-\dfrac{25x^3y^5}{3x}\cdot\dfrac{1}{15xy^2}=\dfrac{-25x^3y^5}{45x^2y^2}=-\dfrac{5}{9}xy^3\)

c: \(=\dfrac{5\left(x-1\right)}{\left(x+1\right)^2}\cdot\dfrac{3\left(x+1\right)}{20\left(x-1\right)\left(x+1\right)}=\dfrac{3}{4\left(x+1\right)^2}\)

d: \(=\dfrac{x\left(x+y\right)}{5\left(x-y\right)\left(x+y\right)}\cdot\dfrac{3\left(x^2+y^2\right)}{x\left(x-y\right)}=\dfrac{3\left(x^2+y^2\right)}{5}\)

\(\left(-\dfrac{30x^2y^2}{7z}\right):\left(-\dfrac{24x^3y}{35z^2}\right)\)

\(=\dfrac{30x^2y^2}{7x}.\dfrac{35z^2}{24x^3y}\)

\(=\dfrac{1050x^2y^2z^2}{168x^4y}=\dfrac{25yz}{4x^2}\)

a: \(=\dfrac{\left(x-y\right)\left(x+y\right)}{x^2+y^2}\cdot\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x-y\right)^2}=\dfrac{\left(x+y\right)^2}{x^2+y^2}\)

b: \(=\dfrac{x^2-xy+y^2}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{\left(x-y\right)^2}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{x-y}{\left(x+y\right)^2}\)

c: \(=y\left(x+y-1\right)\cdot\dfrac{\left(x-y\right)}{x\left(x+y-1\right)}=\dfrac{y\left(x-y\right)}{x}\)

mờ quá

\(A=\dfrac{x\left(x-y\right)}{y}\cdot\dfrac{y\left(x+y\right)}{x\left(x-y\right)}\cdot\dfrac{x^2+1}{x^2+2}=\dfrac{x^2+1}{x^2+2}\)

\(B=\dfrac{x-1}{3x}\cdot\dfrac{x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^2+x+1}{\left(x+1\right)^2}\)

\(=\dfrac{1}{3}\cdot\dfrac{\left(x^2+x+1\right)}{x+1}=\dfrac{x^2+x+1}{3x+3}\)

a: \(=\dfrac{x\left(x-y\right)}{y}\cdot\dfrac{y\left(x+y\right)}{x\left(x-y\right)}\cdot\dfrac{x^2+2}{x^2-1}=\dfrac{\left(x+y\right)\left(x^2+2\right)}{x^2-1}\)

b: \(=\dfrac{x^2+1}{3x}\cdot\dfrac{x-1}{x^2+1}\cdot\dfrac{x\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{\left(x+1\right)^2}\)

\(=\dfrac{x-1}{3x}\cdot\dfrac{x}{x-1}\cdot\dfrac{1}{\left(x+1\right)^2}\)

\(=\dfrac{1}{3\left(x+1\right)^2}\)

c: \(=\dfrac{x^2+y}{y}:\left(\dfrac{z}{x^2}\cdot\dfrac{x^2+y}{xy}\right)\)

\(=\dfrac{x^2+y}{y}\cdot\dfrac{x^3y}{\left(x^2+y\right)z}=\dfrac{x^3}{z}\)

a: \(=\dfrac{xy^2}{2xy}-\dfrac{4}{3}:2\cdot\dfrac{x^2y^3}{xy}+\dfrac{6}{5}:2\cdot\dfrac{x^3y^2}{xy}\)

\(=\dfrac{1}{2}y-\dfrac{2}{3}xy+\dfrac{3}{5}x^2y\)

b: \(=x^3:\dfrac{-1}{3}x+3x^2y:\dfrac{1}{3}x-5xy^2:\dfrac{1}{3}x=-3x^3+9xy-15y^2\)

c: \(=\dfrac{3}{4}:\dfrac{3}{5}\cdot\dfrac{a^3b^6c^2}{a^3bc}+\dfrac{6}{5}:\dfrac{3}{5}\cdot\dfrac{a^4b^3c}{a^3bc}-\dfrac{9}{10}:\dfrac{3}{5}\cdot\dfrac{a^5b^2c^3}{a^3bc}\)

\(=\dfrac{5}{4}b^5c+2ab^2-\dfrac{3}{2}a^2bc^2\)

d: \(=\dfrac{3\left(a-b\right)^5}{3\left(a-b\right)^2}-\dfrac{6\left(a-b\right)^4}{3\left(a-b\right)^2}-\dfrac{21\left(a-b\right)^3}{3\left(a-b\right)^2}+\dfrac{9\left(a-b\right)^2}{3\left(a-b\right)^2}\)

\(=\left(a-b\right)^3-2\left(a-b\right)^2-7\left(a-b\right)+3\)

a, \(=\dfrac{1}{2}y-\dfrac{2}{3}xy^2+\dfrac{3}{5}x^2y\)

b, \(=-3x^2+9xy-15y^2\)

c, \(=\dfrac{5}{4}b^3c+2ab^2-\dfrac{3}{2}a^2bc^2\)

d, \(=\left(a-b\right)^3-2\left(a-b\right)^2-7\left(a-b\right)+3\)

a) \(\dfrac{1}{2}y-\dfrac{2}{3}xy^2+\dfrac{3}{5}x^2y\)

b)\(-3x^2+9xy-15y^2\)

c)\(\dfrac{5}{4}b^5c+2ab^2-\dfrac{3}{2}a^2bc^2\)

d)\(\left(a-b\right)^3-2\left(a-b\right)^2+7\left(a-b\right)+3\)

\(\dfrac{9x-2+2x+2}{x-3}=\dfrac{11x}{x-3}\)

\(=\dfrac{11x}{x-3}\)

\(\dfrac{9x-2+2x+2}{x-3}\)=\(\dfrac{11x}{x-3}\)

Đề bài yêu cầu gì thế em?

`x^2 +4xy+ 4y^2 -9`

`= (x^2 + 2x.2y + 4y^2) -9`

`= (x+2y)^2 - 3^2`

`= (x+2y  -3)(x+2y +3)`

x² + 4xy + 4y² - 9 

= (x² + 4xy + 4y²)-3²

= (x+2y)² - 3²

= (x+2y-3).(x+2y+3)