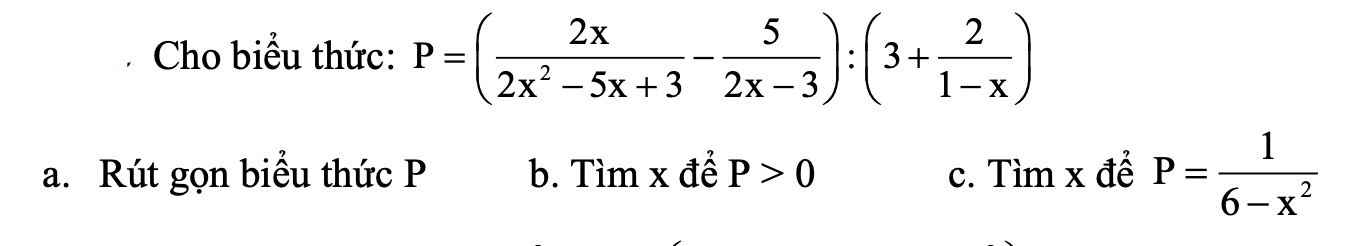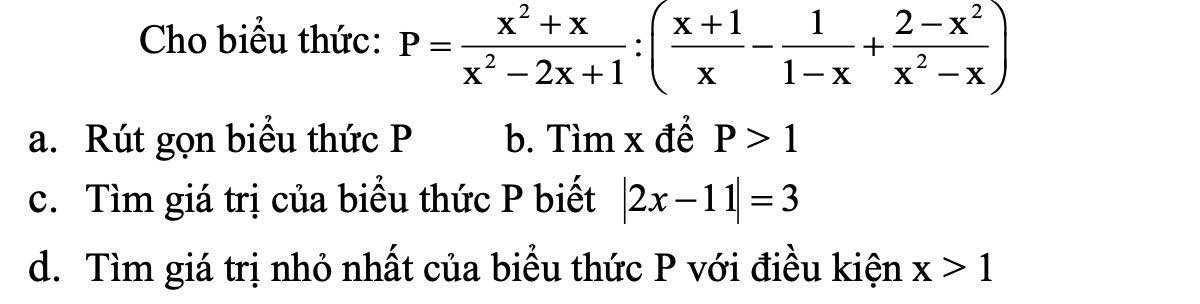Bài 8: Phép chia các phân thức đại số

\(PT\Leftrightarrow2\left(x+7\right)-x\left(x+7\right)=0\)

\(\Leftrightarrow\left(x+7\right)\left(2-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+7=0\\2-x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-7\\x=2\end{matrix}\right.\)

Vậy: \(S=\left\{-7;2\right\}\)

<=>\(\left(x-1\right)\left(x+7\right)=0\)

<=>\(\left[{}\begin{matrix}x-1=0\\x+7=0\end{matrix}\right.\)

<=>\(\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)

<=> x^2+6x+9-16

<=>(x+3)^2-4^2=0

<=>( x+3-4).(x+3+4)=0

<=>x-1=0

x+7=0

<=>x=1 hoặc x=-7

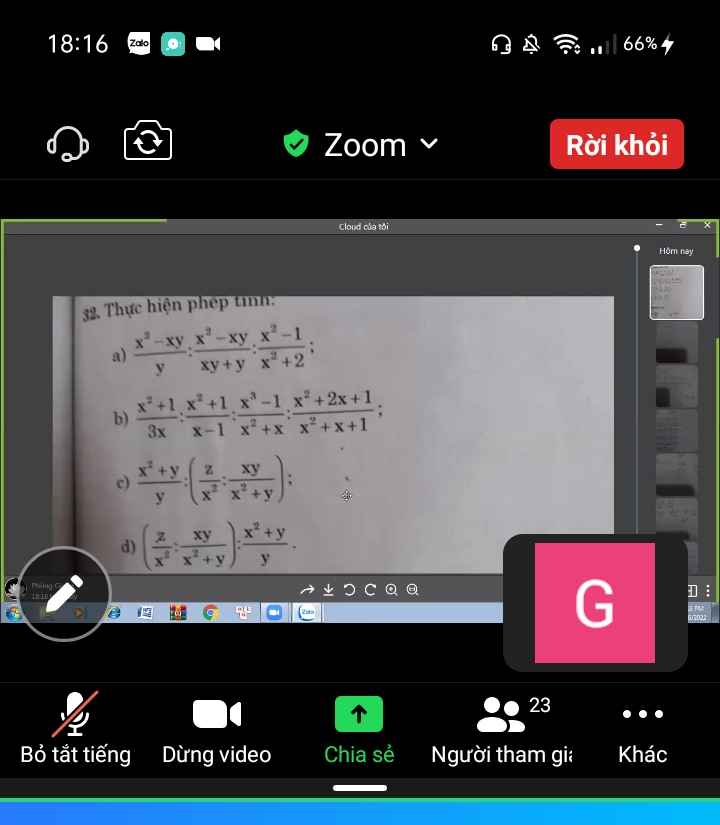
a: \(=\dfrac{x\left(x-y\right)}{y}\cdot\dfrac{y\left(x+y\right)}{x\left(x-y\right)}\cdot\dfrac{x^2+2}{x^2-1}=\dfrac{\left(x+y\right)\left(x^2+2\right)}{x^2-1}\)

b: \(=\dfrac{x^2+1}{3x}\cdot\dfrac{x-1}{x^2+1}\cdot\dfrac{x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^2+x+1}{\left(x+1\right)^2}\)

\(=\dfrac{\left(x^2+x+1\right)}{3\left(x+1\right)^2}\)

c: \(=\dfrac{x^2+y}{y}:\left(\dfrac{z}{x^2}\cdot\dfrac{x^2+y}{xy}\right)\)

\(=\dfrac{x^2+y}{y}\cdot\dfrac{x^3y}{z\left(x^2+y\right)}=\dfrac{x^3}{z}\)

a: \(P=\left(\dfrac{2x}{\left(2x-3\right)\cdot\left(x-1\right)}-\dfrac{5}{2x-3}\right):\left(3-\dfrac{2}{x-1}\right)\)

\(=\dfrac{2x-5x+5}{\left(2x-3\right)\left(x-1\right)}:\dfrac{3x-3-2}{x-1}\)

\(=\dfrac{-3x+5}{\left(2x-3\right)\left(x-1\right)}\cdot\dfrac{x-1}{3x-5}=\dfrac{-1}{2x-3}\)

b: Để P>0 thì 2x-3<0

hay x<3/2

c: Để \(P=\dfrac{-1}{x^2-6}\)  thì \(x^2-6=2x-3\)

\(\Leftrightarrow x^2-2x-3=0\)

=>(x-3)(x+1)=0

=>x=3 hoặc x=-1

a: \(P=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)

\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)

b: Để P>1 thì P-1>0

\(\Leftrightarrow\dfrac{x^2-x+1}{x-1}>0\)

=>x-1>0

hay x>1

c: Ta có: |2x-11|=3

=>2x-11=3 hoặc 2x-11=-3

=>2x=14 hoặc 2x=8

=>x=7 hoặc x=4

Khi x=7 thì \(P=\dfrac{7^2}{7-1}=\dfrac{49}{6}\)

Khi x=4 thì \(P=\dfrac{4^2}{4-1}=\dfrac{16}{3}\)

\(\dfrac{6x^3-7x^2-x+2}{2x+1}\)

\(=\dfrac{6x^3+3x^2-10x^2-5x+4x+2}{2x+1}=3x^2-5x+2\)

=>2x^4+2x^2+3x^3+3x-5x^2-5+mx+n+5 chia hết cho x^2+1

=>mx+n+5=0

=>m=0 và n=-5

cậu ghi đề bài cụ thể hơn đc ko để vậy nhìn rối lắm

\(\dfrac{2x^4-x^3+3x^2+4x+9}{x^2+1}=\dfrac{2x^4+2x^2-x^3-x+x^2+1+5x+8}{x^2+1}\)

\(=2x^2-x+1+\dfrac{5x+8}{x^2+1}\)

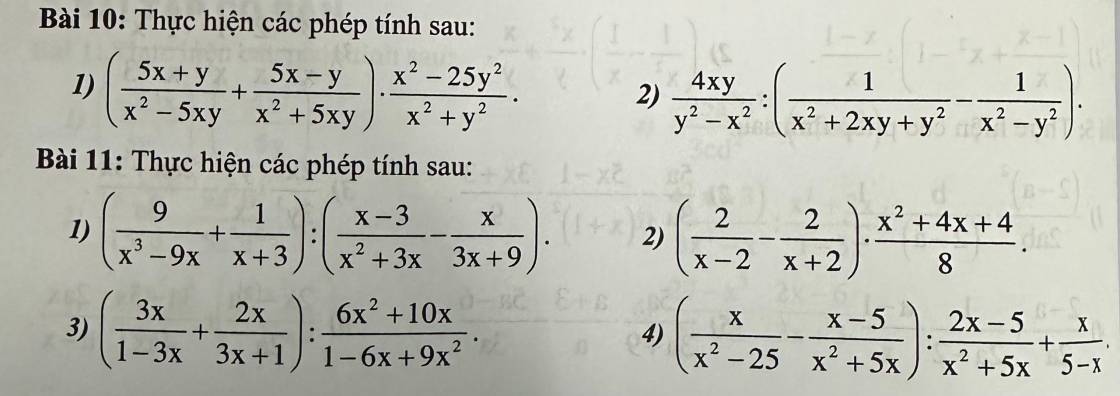
Bài 10:

1: \(\left(\dfrac{5x+y}{x^2-5xy}+\dfrac{5x-y}{x^2+5xy}\right)\cdot\dfrac{x^2-25y^2}{x^2+y^2}\)

\(=\left(\dfrac{5x+y}{x\left(x-5y\right)}+\dfrac{5x-y}{x\left(x+5y\right)}\right)\cdot\dfrac{\left(x-5y\right)\cdot\left(x+5y\right)}{x^2+y^2}\)

\(=\dfrac{\left(5x+y\right)\left(x+5y\right)+\left(5x-y\right)\left(x-5y\right)}{x\left(x-5y\right)\left(x+5y\right)}\cdot\dfrac{\left(x-5y\right)\left(x+5y\right)}{x^2+y^2}\)

\(=\dfrac{5x^2+25xy+xy+5y^2+5x^2-25xy-xy+5y^2}{x\left(x^2+y^2\right)}\)

\(=\dfrac{10x^2+10y^2}{x\left(x^2+y^2\right)}=\dfrac{10\left(x^2+y^2\right)}{x\left(x^2+y^2\right)}=\dfrac{10}{x}\)

2: \(\dfrac{4xy}{y^2-x^2}:\left(\dfrac{1}{x^2+2xy+y^2}-\dfrac{1}{x^2-y^2}\right)\)

\(=\dfrac{-4xy}{\left(x-y\right)\left(x+y\right)}:\left(\dfrac{1}{\left(x+y\right)^2}-\dfrac{1}{\left(x-y\right)\left(x+y\right)}\right)\)

\(=\dfrac{-4xy}{\left(x-y\right)\left(x+y\right)}:\dfrac{x-y-x-y}{\left(x-y\right)\left(x+y\right)^2}\)

\(=\dfrac{-4xy}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{\left(x-y\right)\left(x+y\right)^2}{-2y}\)

\(=2x\left(x+y\right)\)

Bài 11:

1: ĐKXĐ: \(x\notin\left\{0;3;-3\right\}\)

\(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)

\(=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{3\left(x+3\right)}\right)\)

\(=\dfrac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)

\(=\dfrac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{-\left(x^2-3x+9\right)}\)

\(=\dfrac{-3}{x-3}\)

2: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)

\(\left(\dfrac{2}{x-2}-\dfrac{2}{x+2}\right)\cdot\dfrac{x^2+4x+4}{8}\)

\(=\left(\dfrac{2x+4-2x+4}{\left(x-2\right)\left(x+2\right)}\right)\cdot\dfrac{\left(x+2\right)^2}{8}\)

\(=\dfrac{8\left(x+2\right)^2}{8\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)

3: ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{1}{3};0;-\dfrac{5}{3}\right\}\)

\(\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\dfrac{6x^2+10x}{1-6x+9x^2}\)

\(=\left(\dfrac{-3x}{3x-1}+\dfrac{2x}{3x+1}\right)\cdot\dfrac{\left(3x-1\right)^2}{2x\left(3x+5\right)}\)

\(=\dfrac{-3x\left(3x+1\right)+2x\left(3x-1\right)}{\left(3x-1\right)\left(3x+1\right)}\cdot\dfrac{\left(3x-1\right)^2}{2x\left(3x+5\right)}\)

\(=\dfrac{-9x^2-3x+6x^2-2x}{\left(3x+1\right)}\cdot\dfrac{3x-1}{2x\left(3x+5\right)}\)

\(=\dfrac{-x\left(3x+5\right)}{\left(3x+1\right)}\cdot\dfrac{3x-1}{2x\left(3x+5\right)}=\dfrac{-3x+1}{2\left(3x+1\right)}\)

4: ĐKXĐ: \(x\notin\left\{0;5;-5\right\}\)

\(\left(\dfrac{x}{x^2-25}-\dfrac{x-5}{x^2+5x}\right):\dfrac{2x-5}{x^2+5x}+\dfrac{x}{5-x}\)

\(=\left(\dfrac{x}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{x\left(x+5\right)}\right)\cdot\dfrac{x\left(x+5\right)}{2x-5}+\dfrac{x}{5-x}\)

\(=\dfrac{x^2-\left(x-5\right)^2}{x\left(x-5\right)\left(x+5\right)}\cdot\dfrac{x\left(x+5\right)}{2x-5}-\dfrac{x}{x-5}\)

\(=\dfrac{\left(x-x+5\right)\left(x+x-5\right)}{\left(x-5\right)\left(2x-5\right)}-\dfrac{x}{x-5}\)

\(=\dfrac{5}{x-5}-\dfrac{x}{x-5}=\dfrac{5-x}{x-5}=-1\)