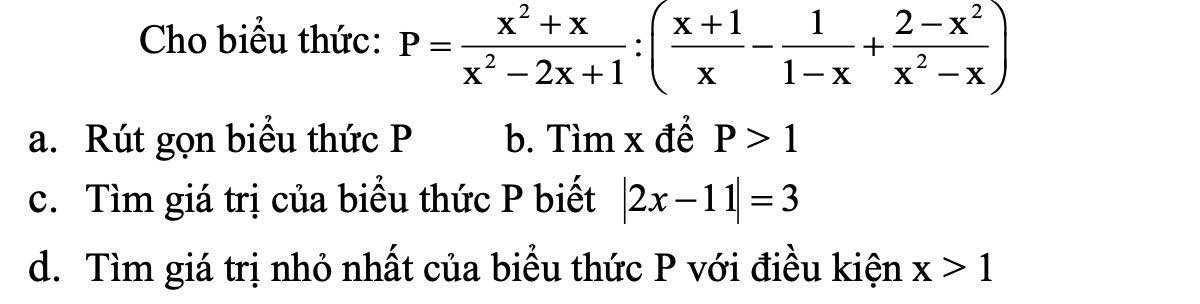a: \(P=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)
b: Để P>1 thì P-1>0
\(\Leftrightarrow\dfrac{x^2-x+1}{x-1}>0\)
=>x-1>0
hay x>1
c: Ta có: |2x-11|=3
=>2x-11=3 hoặc 2x-11=-3
=>2x=14 hoặc 2x=8
=>x=7 hoặc x=4
Khi x=7 thì \(P=\dfrac{7^2}{7-1}=\dfrac{49}{6}\)
Khi x=4 thì \(P=\dfrac{4^2}{4-1}=\dfrac{16}{3}\)
Đúng 1
Bình luận (0)
