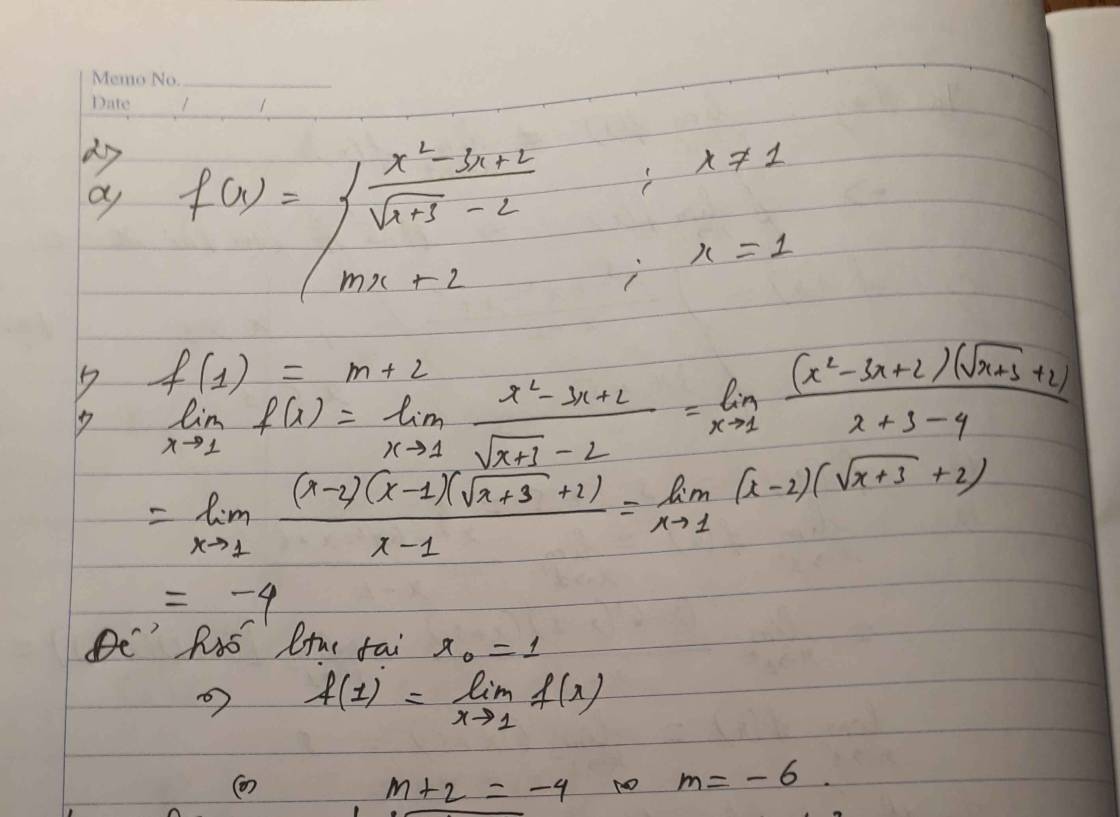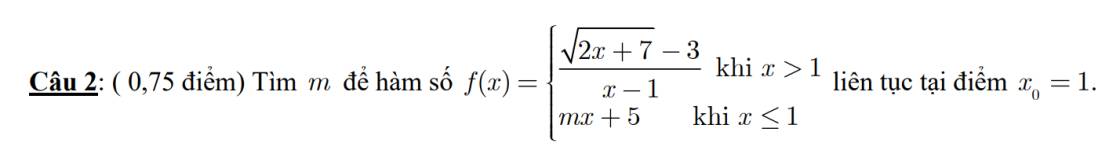Chứng minh rằng: \(m.\left(1-x\right)^3.\left(x^2-4\right)+x^4-3=0\) có ít nhất 2 nghiệm với mọi m
Bài 3: Hàm số liên tục
Đặt f(x) = m(1 - x)³.(x² - 4) + x⁴ - 3
⇒ f(x) liên tục trên R
Ta có:
f(-2) = m.(1 - 2)³.[(-2)² - 4] + (-2)⁴ - 3
= 0 + 16 - 3
= 15
f(1) = m.(1 - 1)³.(1² - 4) + 1⁴ - 3
= 0 + 1 - 3
= -2
f(2) = m.(1 - 2)³.(2² - 4) + 2⁴ - 3
= 0 + 16 - 3
= 15
Do f(-2).f(1) = 15.(-2) = -30 < 0
Và f(1).f(2) = -2.15 < 0
⇒ Phương trình đã cho có ít nhất 2 nghiệm x₁ và x₂ với mọi m, trong đó x₁ ∈ (-2; 1); x₂ ∈ (1; 2)
Đúng 3
Bình luận (0)
Chứng minh rằng: \(2x+6.\sqrt[3]{1-x}=3\) có 3 nghiệm phân biệt
\(f\left(x\right)=2x+6\sqrt[3]{1-x}-3\) liên tục trên R.
\(f\left(1\right)=-1;f\left(0\right)=3;f\left(-7\right)=-5;f\left(9\right)=3\)
\(f\left(-7\right)f\left(0\right)< 0\) --> f(x) = 0 có 1 nghiệm thuộc khoảng (-7; 0)
\(f\left(0\right)f\left(1\right)< 0\) --> f(x) = 0 có 1 nghiệm thuộc khoảng (0; 1)
\(f\left(1\right)f\left(9\right)< 0\) --> f(x) = 0 có 1 nghiệm thuộc khoảng (1; 9)
Vậy f(x) = 0 có 3 nghiệm phân biệt.
Đúng 2
Bình luận (0)
1/ Xét tính liên tục của hàm số tại một điểm:a) fleft(xright)left{{}begin{matrix}dfrac{x^2-4}{x^2+x-2};xne22x+1;x2end{matrix}right. tại x_02b) fleft(xright)left{{}begin{matrix}left(x+3right)^3-27;x0x^3+27;xle0end{matrix}right. tại x_00c) fleft(xright)left{{}begin{matrix}dfrac{x^3-6x^2-x+6}{x-1};x13x+5;xle1end{matrix}right. tại x_01d) fleft(xright)left{{}begin{matrix}dfrac{sqrt{3x+10}-x-4}{x+2};xne-2-dfrac{1}{4};x-2end{matrix}right. tại x_0-22/ Tìm m để hàm số sau liên tục tại điểm đã chỉ ra:a) ...
Đọc tiếp
1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2};x\ne2\\2x+1;x=2\end{matrix}\right.\) tại \(x_0=2\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\left(x+3\right)^3-27;x>0\\x^3+27;x\le0\end{matrix}\right.\) tại \(x_0=0\)
c) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-6x^2-x+6}{x-1};x>1\\3x+5;x\le1\end{matrix}\right.\) tại \(x_0=1\)
d) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{3x+10}-x-4}{x+2};x\ne-2\\-\dfrac{1}{4};x=-2\end{matrix}\right.\) tại \(x_0=-2\)
2/ Tìm \(m\) để hàm số sau liên tục tại điểm đã chỉ ra:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{\sqrt{x+3}-2};x\ne1\\mx+2;x=1\end{matrix}\right.\) tại \(x_0=1\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt[3]{2x^2=9}-3}{2x-6};x\ne3\\m;x=3\end{matrix}\right.\) tại \(x_0=3\)
1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2},x\ne2\\2x+1,x=2\end{matrix}\right.\left(x_0=2\right)}\)
Đề lỗi công thức toán rồi bạn. Không nhìn thấy được biểu thức hiển thị.
Đúng 0
Bình luận (0)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{2x+7}-3}{x-1}\)
\(=\lim\limits_{x\rightarrow1^+}\dfrac{2x+7-9}{\sqrt{2x+7}+3}\cdot\dfrac{1}{x-1}=\lim\limits_{x\rightarrow1^+}\dfrac{2}{\sqrt{2x+7}+3}\)
\(=\dfrac{2}{\sqrt{2+7}+3}=\dfrac{2}{6}=\dfrac{1}{3}\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}mx+5=m+5\)
f(1)=m*1+5=m+5
Để hàm số liên tục tại x=1 thì m+5=1/3
=>m=-14/3
Đúng 0
Bình luận (0)
Cho hàm số y=f(x)=√x+7 -3∠x-2 , xkhác 2 ; mx+2023 ,x=2 (với m là tham số)
Tìm m để hàm số liên tục tại điểm x=2
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{x+7}-3}{x-2}\left(x< >2\right)\\mx+2023\left(x=2\right)\end{matrix}\right.\)
Để hàm số liên tục tại x=2 thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=F\left(2\right)\)
=>\(\lim\limits_{x\rightarrow2}\dfrac{x+7-9}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=2m+2023\)
=>\(2m+2023=\dfrac{1}{\sqrt{2+7}+3}=\dfrac{1}{6}\)
=>m=-12137/12
Đúng 0
Bình luận (0)
\(f\left(x\right)=\dfrac{\sqrt{\left(x-1\right)^2\left(x+1\right)^2\left(x+2\right)}}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{\left|x-1\right|\sqrt{\left(x+1\right)^2\left(x+2\right)}}{\left(x-1\right)\left(x^2+x+1\right)}\)
Nên;
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\dfrac{\left(x-1\right)\sqrt{\left(x+1\right)^2\left(x+2\right)}}{\left(x-1\right)\left(x^2+x+1\right)}=\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{\left(x+1\right)^2\left(x+2\right)}}{x^2+x+1}=\dfrac{2\sqrt{3}}{3}\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\dfrac{-\left(x-1\right)\sqrt{\left(x+1\right)^2\left(x+2\right)}}{\left(x-1\right)\left(x^2+x+1\right)}=\lim\limits_{x\rightarrow1^-}\dfrac{-\sqrt{\left(x+1\right)^2\left(x+2\right)}}{x^2+x+1}=-\dfrac{2\sqrt{3}}{3}\)
\(\Rightarrow\)\(\lim\limits_{x\rightarrow1^+}f\left(x\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\) nên giới hạn \(\lim\limits_{x\rightarrow1}f\left(x\right)\) ko tồn tại
Đúng 1
Bình luận (0)
2: f(x)=(9-x^2)/(x-3)=-(x+3)
Khi x<3 thì \(lim_{x->3^-}f\left(x\right)=-\left(3+3\right)=-6\)
\(lim_{x->3^+}f\left(x\right)=1-3=-2< >-6\)
=>f(x) bị gián đoạn tại x=3
1:
\(\dfrac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1}=\dfrac{1+x-1}{\sqrt{1+x}+1}:\dfrac{1+x-1}{\sqrt[3]{\left(1+x\right)^2}+\sqrt[3]{1+x}+1}\)
\(=\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt{x+1}+1}\)
\(lim_{x->0^+}f\left(x\right)=\dfrac{\sqrt[3]{\left(0+1\right)^2}+\sqrt[3]{0+1}+1}{\sqrt{0+1}+1}=\dfrac{1+1+1}{1+1}=\dfrac{3}{2}=lim_{x->0^-}f\left(x\right)\)
=>Hàm số liên tục tại x=0
Đúng 0
Bình luận (0)
\(f(x) = \begin{cases} \dfrac{x^2-6x+8}{\sqrt{3x+2}-2} \ khi \ x < 2 \\ \dfrac{x+8}{x-1} \ khi \ x \geq 2 \\\end{cases}
tại x_0 =2.\) Xét tính liên tục của hàm số:
\(\lim\limits_{x->2^-}=\dfrac{2^2-6\cdot2+8}{\sqrt{3\cdot2+2}-2}=0\)
\(\lim\limits_{x->2^+}=\dfrac{2+8}{2-1}=10< >0\)
=>f(x) không liên tục tại x=2
Đúng 0
Bình luận (0)