Lời giải:
\(B=\frac{2x+\sqrt{x}-4}{(\sqrt{x}+1)(\sqrt{x}-2)}-\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{(\sqrt{x}+1)(\sqrt{x}-2)}+\frac{\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}\)
\(=\frac{2x+\sqrt{x}-4-(x-4)+\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{x+2\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{(\sqrt{x}+1)^2}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(P=AB=\frac{3\sqrt{x}-4}{\sqrt{x}+1}.\frac{\sqrt{x}+1}{\sqrt{x}-2}=\frac{3\sqrt{x}-4}{\sqrt{x}-2}\)
\(P\geq 2\Leftrightarrow \frac{3\sqrt{x}-4}{\sqrt{x}-2}\geq 2\)
\(\Leftrightarrow \frac{3\sqrt{x}-4}{\sqrt{x}-2}-2\geq 0\Leftrightarrow \frac{\sqrt{x}}{\sqrt{x}-2}\geq 0\)
\(\Leftrightarrow \sqrt{x}-2>0\Leftrightarrow x>4\)
Kết hợp với ĐKXĐ suy ra $x>4$

 ý c helpppppppppppppp
ý c helpppppppppppppp






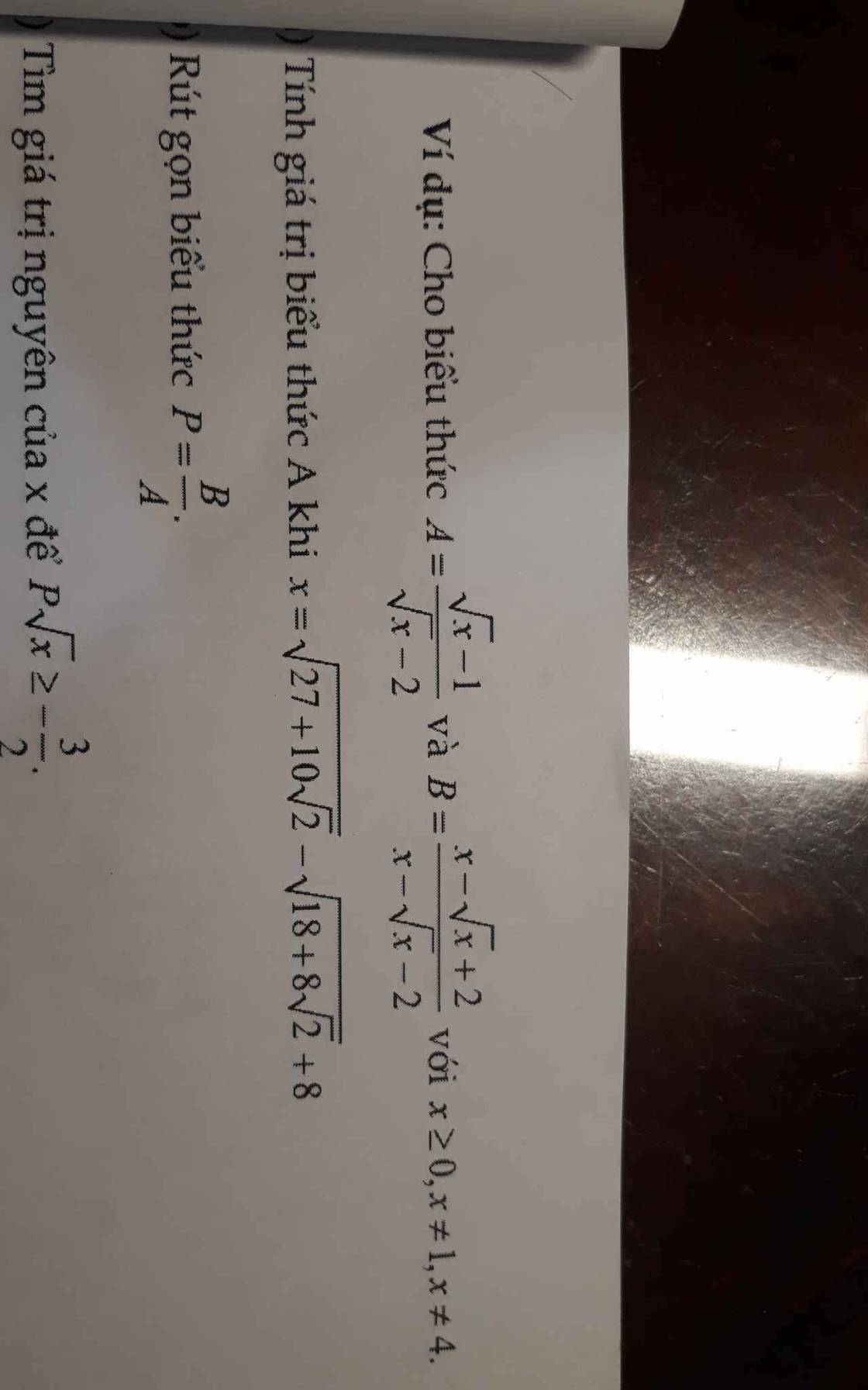 Giúp mình ý c với
Giúp mình ý c với


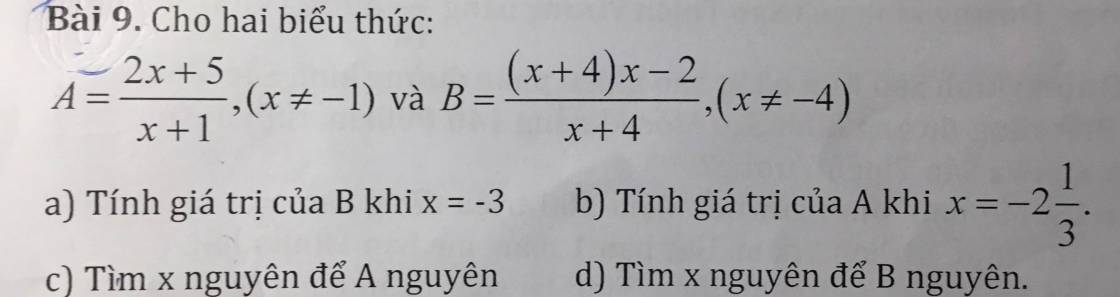





 Làm giúp mk ý c bài 5.5
Làm giúp mk ý c bài 5.5