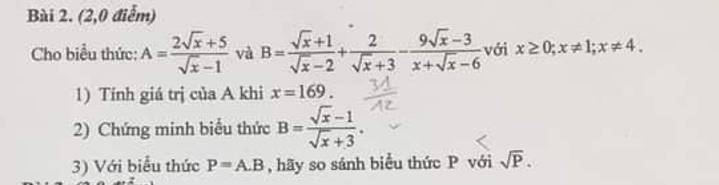a: \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}+8\)
\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}+8\)
\(=5+\sqrt{2}-4-\sqrt{2}+8=9\)
Khi x=9 thì \(A=\dfrac{3-1}{3-2}=\dfrac{2}{1}=2\)
b: \(P=B:A\)
\(=\dfrac{x-\sqrt{x}+2}{x-\sqrt{x}-2}:\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
\(=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\dfrac{x-\sqrt{x}+1}{x-1}\)
c: \(P\cdot\sqrt{x}>=-\dfrac{3}{2}\)
=>\(\dfrac{x\sqrt{x}-x+\sqrt{x}}{x-1}+\dfrac{3}{2}>=0\)
=>\(\dfrac{2x\sqrt{x}-2x+2\sqrt{x}+3x-3}{2\left(x-1\right)}>=0\)
=>\(\dfrac{2x\sqrt{x}+x+2\sqrt{x}-1}{2\left(x-1\right)}>=0\)
TH1: \(\left\{{}\begin{matrix}2x\sqrt{x}+x+2\sqrt{x}-1>=0\\x-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>1\\x>=0,38\end{matrix}\right.\)
=>x>1
=>\(x\in N\backslash\left\{0;1;4\right\}\)
TH2: \(\left\{{}\begin{matrix}2x\sqrt{x}+x+2\sqrt{x}-1< =0\\x-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 1\\x< =0,38\end{matrix}\right.\)
=>0<=x<0,38
mà x nguyên
nên \(x=0\)

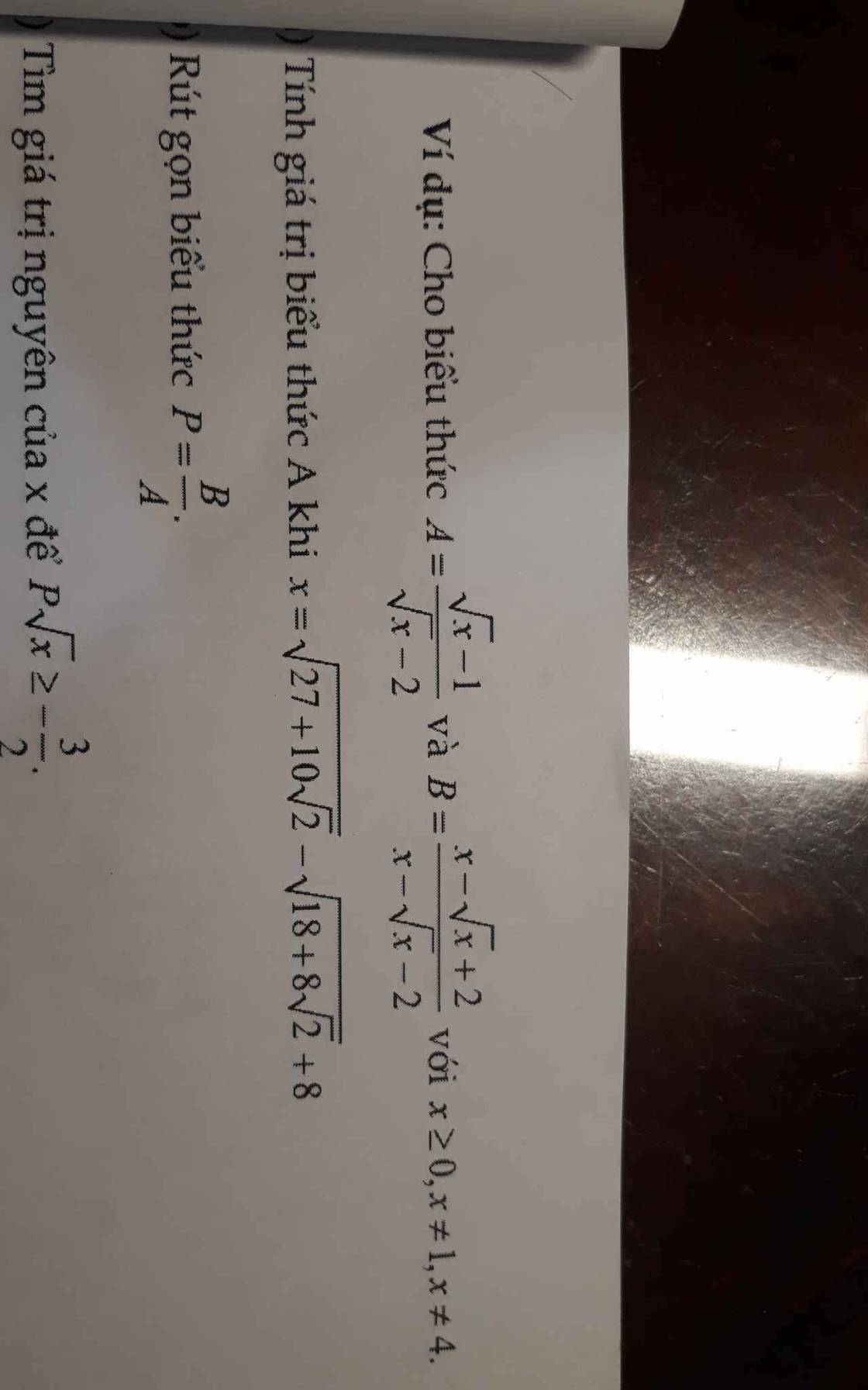 Giúp mình ý c với
Giúp mình ý c với