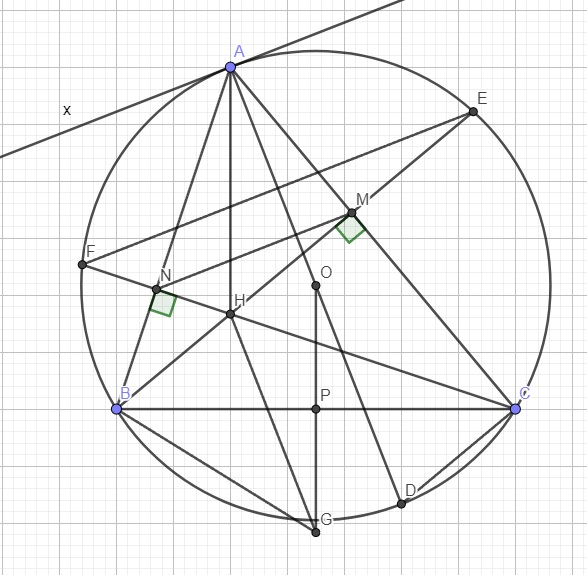
1: Xét tứ giác BNMC có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp
2: Xét (O) có
\(\widehat{CFE}\) là góc nội tiếp chắn cung CE
\(\widehat{CBE}\) là góc nội tiếp chắn cung CE
Do đó: \(\widehat{CFE}=\widehat{CBE}\)
mà \(\widehat{CBE}=\widehat{CNM}\)(BNMC nội tiếp)
nên \(\widehat{CNM}=\widehat{CFE}\)
=>NM//FE
3.
Qua A kẻ tiếp tuyến Ax của (O) \(\Rightarrow OA\perp Ax\) (1)
Ta có: \(\widehat{BAx}=\widehat{BCA}\) (cùng chắn AB) (2)
Theo câu a, BNMC nội tiếp \(\Rightarrow\widehat{BCA}+\widehat{BNM}=180^0\) (3)
Mà \(\widehat{BNM}+\widehat{ANM}=180^0\) (kề bù) (4)
(2);(3);(4) \(\Rightarrow\widehat{BAx}=\widehat{ANM}\)
\(\Rightarrow Ax||MN\) (hai góc so le trong bằng nhau) (5)
(1);(5) \(\Rightarrow OA\perp MN\)
Mà \(d\perp MN\left(gt\right)\Rightarrow d||OA\)
Gọi G là giao điểm của OP và d \(\Rightarrow HG||OA\) (6)
AD là đường kính \(\Rightarrow\widehat{ACD}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow CD\perp AC\)
\(\Rightarrow CD||BH\) (cùng vuông góc AC)
Tương tự ta có \(BD||CH\) (cùng vuông góc AB)
\(\Rightarrow BHCD\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\) Hai đường chéo BC, DH cắt nhau tại trung điểm mỗi đường.
Mà P là trung điểm BC \(\Rightarrow P\) đồng thời là trung điểm DH
\(\Rightarrow OP\) là đường trung bình tam giác ADH
\(\Rightarrow OP||AH\) hay \(OG||AH\) (7)
(6);(7) \(\Rightarrow AHGO\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow OG=AH\)
Theo cmt, OP là đường trung bình tam giác ADH \(\Rightarrow OP=\dfrac{1}{2}AH\)
\(\Rightarrow PG=OG-OP=AH-\dfrac{1}{2}AH=\dfrac{1}{2}AH\)
\(\Rightarrow PG=OP\Rightarrow P\) là trung điểm của OG
Mà O cố định, BC cố định nên P cố định \(\Rightarrow G\) cố định
Vậy khi A di động trên cung lớn BC thì d luôn đi qua điểm G cố định, là điểm đối xứng O qua P



















 vẽ hình luôn ạ
vẽ hình luôn ạ
