Lời giải:
\(\widehat{CSD}=\frac{\text{sđc(CD)}-\text{sđc(MN)}}{2}=\frac{120^0-\text{sđc(MN)}}{2}\)
\(\Rightarrow \text{sđc(MN)}=120^0-2\widehat{CSD}=120^0-2.40^0=40^0\)
Cho (O; R) và dây cung MN = R 3 . Kẻ OK vuông góc với MN tại K. Hãy tính:
a, Độ dài OK theo R
b, Số đó các góc M O K ^ ; M O N ^
c, Số đo cung nhỏ và cung lớn M N ⏜
Cho MN là đáy cung của ( O, R ) và MN bằng R tính số đo MN
Cho ( O;R) và dây cung MN = R căn 3 . Kẻ OK vuông góc với MN tại K . a ) Tính độ dài Ok theo R b) Tính góc MOK và góc MON c) Tính số đo cung nhỏ và cung lớn MN
Cho đường tròn tâm o bán kính R, đường kính MN. Gọi P là điểm chính giữa của cũng MN, vẽ dây PQ = R. Tính số đo góc tâm NOQ Q € cung nhỏ NP
Cho đường tròn tâm O bán kính R đường kính MN. Vẽ dây cung AB =R; MA và NB kéo dài cắt nhau tại E a) Tính số đo cung AB nhỏ và số đo của góc MEN b) Gọi H là giao điểm của MB và NA. Chứng minh tứ giác EAHB nội tiếp c) Chứng minh MH.MB+NH.NA = 4R bình phương
Vẽ hình + giải luôn ạ
Cho điểm A nằm ngoài đường tròn tâm O,kẻ hai tiếp tuyến AM,AN của đường tròn (MN là tiếp điểm).Biết góc MAN=60 độ.
a)Tính góc ở tâm MON.
b)Tính số đo các cung MN.
Cho em xin lời giải cụ thể với ạ.Em cảm ơn
Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB.
Từ đó, tính số đo cung AnB tương ứng.
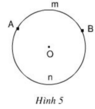
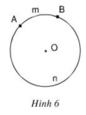
Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB.
Từ đó, tính số đo cung AnB tương ứng.
