Xét ΔPOQ có OP=OQ=PQ
nên ΔOPQ đều
=>góc POQ=60 độ
=>góc NOQ=30 độ
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho đường tròn tâm O bán kính R đường kính MN. Vẽ dây cung AB =R; MA và NB kéo dài cắt nhau tại E a) Tính số đo cung AB nhỏ và số đo của góc MEN b) Gọi H là giao điểm của MB và NA. Chứng minh tứ giác EAHB nội tiếp c) Chứng minh MH.MB+NH.NA = 4R bình phương
Cho đường tròn tâm O đường kính AB. Trên bán kính OA, lấy điểm C tùy ý (C khác O và A). Vẽ đường tròn tâm J đường kính AC. Gọi I là trung điểm BC. Qua I vẽ dây cung MN vuông góc BC; AM cắt đường tròn tâm J tại E.a/ CM CIME nội tiếp.b/ CM BMCN là hình thoi. Từ đó suy ra ba điểm E, C, N cùng thuộc một đường thẳng.c/ CM IE là tiếp tuyến của đường tròn tâm J.d/ Đường tròn tâm M bán kính MI cắt đường tròn tâm O tại P và Q, Gọi H là giao điểm của PQ và MN. Tính tỉ số HM/HN
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Trên bán kính OA, lấy điểm C tùy ý (C khác O và A). Vẽ đường tròn tâm J đường kính AC. Gọi I là trung điểm BC. Qua I vẽ dây cung MN vuông góc BC; AM cắt đường tròn tâm J tại E.
a/ CM CIME nội tiếp.
b/ CM BMCN là hình thoi. Từ đó suy ra ba điểm E, C, N cùng thuộc một đường thẳng.
c/ CM IE là tiếp tuyến của đường tròn tâm J.
d/ Đường tròn tâm M bán kính MI cắt đường tròn tâm O tại P và Q, Gọi H là giao điểm của PQ và MN. Tính tỉ số HM/HN
Cho đường tròn (O;R), đường kính AB .Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm BOD. Có mấy đáp số
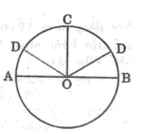
Cho đường tròn (O; R), đường kính AB. Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm DOB. Có mấy đáp số ?
Cho ( O; R) đường kính AB . Gọi C là điểm chính giữa cung AB. Vẽ dây CD= R( D thuộc cung BC nhỏ) . Tính góc ở tâm BOD
Cho đường tròn tâm O bán kính R điểm M nằm ngoải đường tròn sao cho OM=2R. V ẽ trung tuyến MA gọi PQ là giao điểm của đường tròn tâm O với MO . P nằm giũa M và O.
a) Tính số đo góc AOQ
b) Tính số đo cung nhỏ AQ và cung lớn AQ
Cho đường tròn tâm O bán kính R, dây AB không qua tâm O, I là trung điểm của AB. AB dài 16cm, bán kính R= 10 cm
a) Tính OI
b) OI cắt đường tròn O tại M . Tính AM
c) Kẻ đường kính MN của đường tròn tâm O, kẻ OK vuông góc với AN tại K. Tính AK
) Cho đường tròn tâm O bán kính OA và dây cung MN vuông góc OA (A nằm trên cung nhỏ MN). Vẽ dây cung AB và dây cung AC sao cho AB cắt MN tại I, AC cắt MN tại K theo thứ tự M, I, K, N. 1/ Chứng minh: Tứ giác BIKC nội tiếp. 2/ Gọi R là giao của AB và MC, S là giao của AC và BN. Chứng minh: MN // RS và AB.IR AC.KS. 3/ Chứng minh: MA là tiếp tuyến của đường tròn ngoại tiếp MBI và đường tròn ngoại tiếp MBI tiếp xúc với đường tròn ngoại tiếp MCK.
Đọc tiếp
) Cho đường tròn tâm O bán kính OA và dây cung MN vuông góc OA (A nằm trên cung nhỏ MN). Vẽ dây cung AB và dây cung AC sao cho AB cắt MN tại I, AC cắt MN tại K theo thứ tự M, I, K, N. 1/ Chứng minh: Tứ giác BIKC nội tiếp. 2/ Gọi R là giao của AB và MC, S là giao của AC và BN. Chứng minh: MN // RS và AB.IR = AC.KS. 3/ Chứng minh: MA là tiếp tuyến của đường tròn ngoại tiếp MBI và đường tròn ngoại tiếp MBI tiếp xúc với đường tròn ngoại tiếp MCK.
Cho đường tròn tâm O bán kính R ,dây MN khác đường kính.Hai tiếp tuyến của đường tròn(O;R) tại M và tại N cắt nhau tại S.Kẻ đường kính NP,kẻ MQ vuông góc với NP tại Q
a)Chứng minh:SO vuông góc với MN
b)Cho biết R=15cm,MN=24cm.Tính SM,SO
c)Chứng minh:MN là tia phân giác của góc SMQ
d)Goi J là giao điểm của SP và MQ.Chứng minh JQ=JM