b: \(=-cos\left(3\cdot10\right)=-cos30=-\dfrac{\sqrt{3}}{2}\)
c: \(=\dfrac{1}{2}\cdot\left(2-4\cdot\dfrac{2+\sqrt{3}}{4}\right)\)
=-căn 3/2
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
1/ Cho \(cot\alpha=\sqrt{5}\) . Tính \(C=sin^2\alpha-sin\alpha cos\alpha+cos^2\alpha\)
2/ Cho \(tan\alpha=3\) . Tính \(B=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}\)
1 tháng 10 2021 lúc 9:12
a)4sin^3xcos3x+4cos^3xsin3x+3sqrt{3}cos4x3b)2sin^2xleft(4sin^4x-1right)cos2xleft(7cos^22x+3cos2x-4right)2 câu này giải như nào ạ
Đọc tiếp
a)\(4sin^3xcos3x+4cos^3xsin3x+3\sqrt{3}cos4x=3\)
b)\(2sin^2x\left(4sin^4x-1\right)=cos2x\left(7cos^22x+3cos2x-4\right)\)
2 câu này giải như nào ạ
Cho cot x = \(\sqrt{2}\) . tính giá trị biểu thức sau P=\(\dfrac{3sinx-2cosx}{12sin^3x+4cos^3x}\)
Tính tổng tất cả các nghiệm của phương trình
3
cos
x
-
sin
x
1
trên đoạn
0
;
2
π
A.
5
π
3
B.
11
π...
Đọc tiếp
Tính tổng tất cả các nghiệm của phương trình 3 cos x - sin x = 1 trên đoạn 0 ; 2 π
A. 5 π 3
B. 11 π 6
C. π 6
D. 3 π 2
1.cho cotx = -6 tính F = \(\dfrac{sinx-3cosx}{cosx+2sinx}\)
2. cho cotx = 1 tính I = \(\dfrac{sin^3x-4cos^3x}{sinx+3cosx}\)
3. cho cotx = 3 tính I = \(\dfrac{2sin^3x+cos^3x}{4sinx-6cosx}\)
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Biến đổi phương trình sau cos3x-sinx
3
(cosx-sin3x) về dạng sin(ax+b)sin(cx+d) với b, d thuộc khoảng
-
π
2
;
π
2
. Tính chính xác giá trị của b+d ?
Đọc tiếp
Biến đổi phương trình sau cos3x-sinx= 3 (cosx-sin3x) về dạng sin(ax+b)=sin(cx+d) với b, d thuộc khoảng - π 2 ; π 2 . Tính chính xác giá trị của b+d ?
1) cho góc x (0 độ le x 90 độ) thỏa mãn sinxdfrac{4}{5} giá trị của tanx là 2) cho góc x (0 độ le x le 180 độ) thỏa mãn cosxdfrac{1}{3} giá trị của sinx là3) cho cosxdfrac{1}{2} tính P3sin^2x+4cos^2x
Đọc tiếp
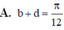
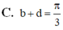
1) cho góc x (0 độ \(\le\) x < 90 độ) thỏa mãn \(sinx=\dfrac{4}{5}\) giá trị của \(tanx\) là
2) cho góc x (0 độ \(\le\) x \(\le\) 180 độ) thỏa mãn \(cosx=\dfrac{1}{3}\) giá trị của \(sinx\) là
3) cho \(cosx=\dfrac{1}{2}\) tính \(P=3sin^2x+4cos^2x\)
a) \(sinx=-\dfrac{6}{5}\)
b) \(sin3x=\dfrac{\sqrt{3}}{2}\)
c) \(sin\left(x+\dfrac{\pi}{3}\right)=sin\dfrac{3\pi}{4}\)
d) \(4sin\left(x+\dfrac{5\pi}{6}\right)=5\)