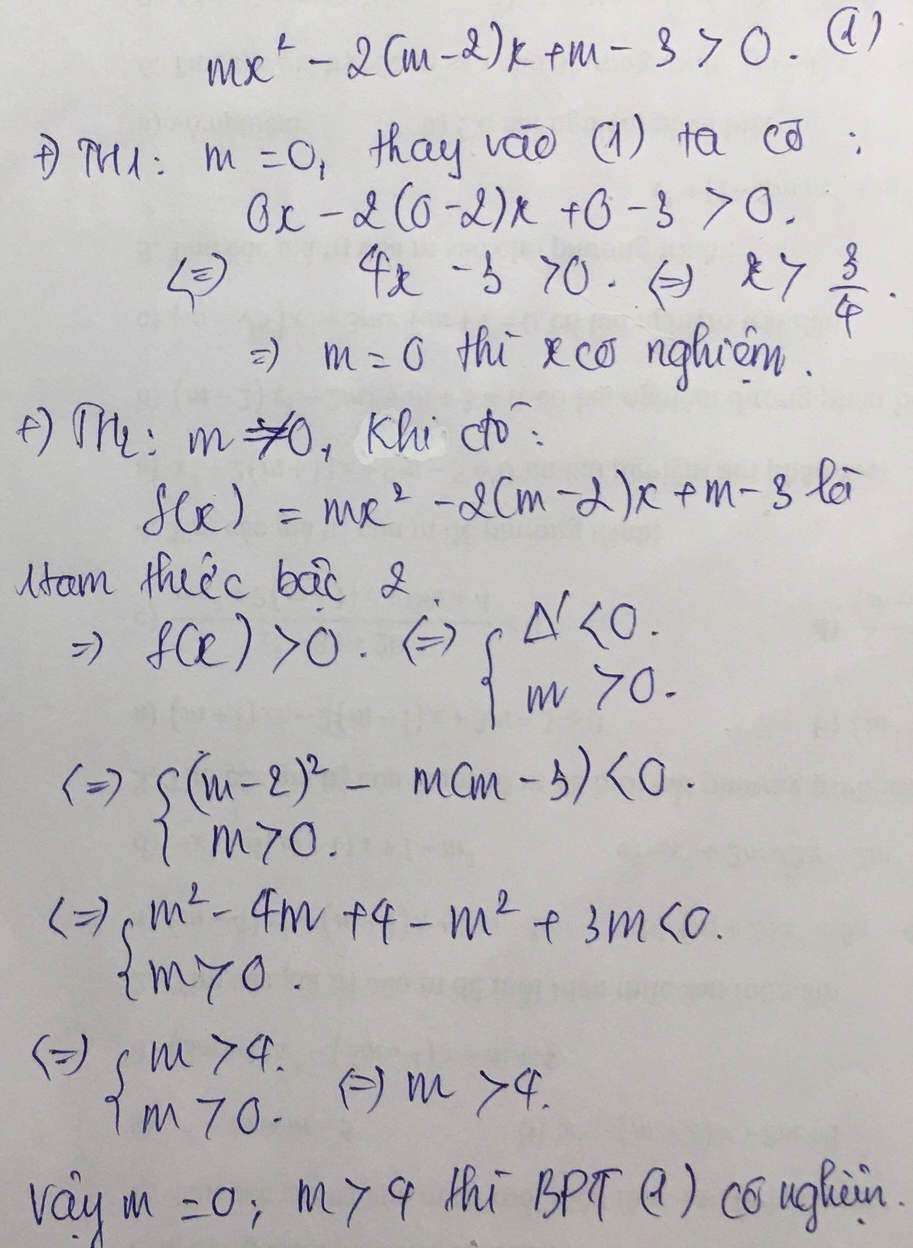Trường hợp 1: m=0
Bất phương trình trở thành:
\(-2\cdot\left(0-2\right)x+0-3>0\)
=>4x-3>0
hay x>3/4
=>Nhận trường hợp m=0
Trường hợp 2: m<>0
\(\text{Δ}=\left(2m-4\right)^2-4m\left(m-3\right)\)
\(=4m^2-16m+16-4m^2+12m\)
=-4m+16
Để phương trình có nghiệm thì \(\left\{{}\begin{matrix}-4m+16< 0\\m>0\end{matrix}\right.\Leftrightarrow m>4\)
Vậy: m>4
Với \(m=0\) thỏa mãn
Với \(m\ne0\) BPT vô nghiệm khi: \(mx^2-2\left(m-2\right)x+m-3\le0\) nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-2\right)^2-m\left(m-3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m\ge4\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m để BPT đã cho vô nghiệm
\(\Rightarrow\) BPT đã cho có nghiệm với mọi m