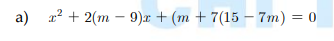\(x^2+2\left(m-9\right)x+\left(m+7\right)\left(15-7m\right)=0\)
Để phương trình có đúng một nghiệm thì \(\left[2\left(m-9\right)\right]^2-4\left(m+7\right)\left(15-7m\right)=0\)
=>\(4\left(m-9\right)^2-4\left(m+7\right)\left(15-7m\right)=0\)
=>\(\left(m-9\right)^2-\left(m+7\right)\left(15-7m\right)=0\)
=>\(m^2-18m+81-15m+7m^2-105+49m=0\)
=>\(8m^2+16m-24=0\)
=>\(m^2+2m-3=0\)
=>(m+3)(m-1)=0
=>\(\left[{}\begin{matrix}m=-3\\m=1\end{matrix}\right.\)